《固体物理学》作业02
提交时间:3月5日, 周2, 课前
1. 任意维度德拜模型
请计算
的声子态密度. 计算其低温极限对比热容
2. 点群对称性
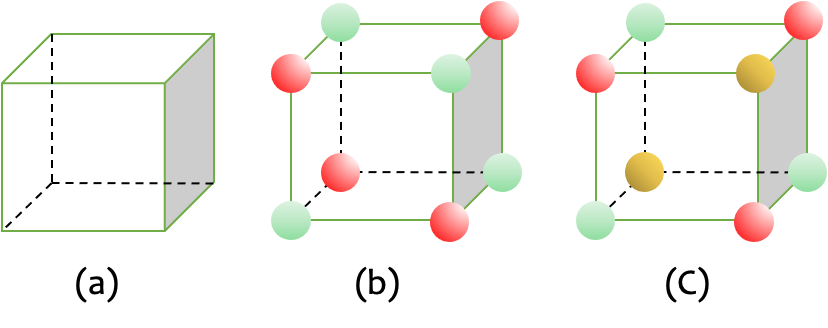
下图中绿边所示的多面体为均匀立方体(灰色面和虚线仅用来展示立体感, 对对称性没有影响), 彩球为均匀球体, 球心位于立方体的顶角处. 不同颜色的彩球视为不同. 试列举:
(b)比(a)缺失的点群对称性;
(c)比(b)缺失的点群对称性.
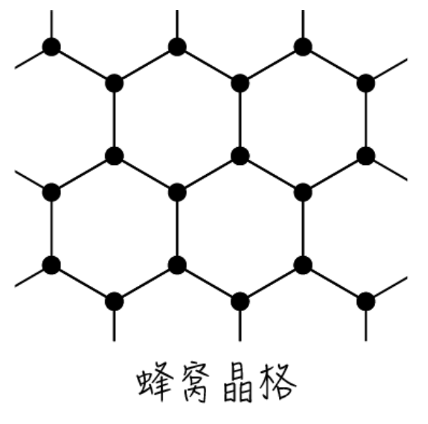
3. 蜂窝晶格
如图所示的蜂窝晶格是不是2维布拉维格子?为什么?作出这一结构的二维布拉维格子和元胞.
4. 三维布拉维格子
设格矢
(a)
(b)
5. 简要解释为什么
(a) 四方晶系没有底心或者面心的情形?
(b) 立方晶系没有底心的情形?
(c)六方晶系没有任何一种心的情形?
6. 晶面族间距
请给出六方晶系中弥勒指数为