Lecture 2

02/23/23, Th.

Today

Hartree-Fock approximation
Density functional theory; Kohn-Sham equations
Density response and screening

Reading: GY 15.1 -- 15.3.

1. The Hartree-Fock approximation

General many-electron Hamiltonian

\begin{matrix} (1) & \hat{H} = \hat{T} + \hat{V} + \hat{U} . \end{matrix}

Determinantal wavefunction

\begin{matrix} (2) & Ψ (r_{1} σ_{1} \dots r_{N} σ_{N}) = \frac{1}{\sqrt{N!}} \sum_{P \in S_{N}} sgn (P) φ_{P_{1}} (r_{1} σ_{1}) \dots φ_{P_{N}} (r_{N} σ_{N}) \end{matrix}

The Hartree-Fock approximation can be formulated as a variational problem in the single-determinant Hilbert space

\begin{matrix} (3) & E_{HF} = min_{{φ_{i}}} ⟨ Ψ | \hat{H} | Ψ ⟩, subject to ⟨ φ_{i} | φ_{j} ⟩ = δ_{i j} \end{matrix}

The Hartree-Fock Lagrangian (拉氏量)

\begin{matrix} (4) & L_{HF} = ⟨ Ψ | \hat{H} | Ψ ⟩ - λ_{i j} (⟨ φ_{i σ} | φ_{j σ^{'}} ⟩ - δ_{i j} δ_{σ σ^{'}}) \end{matrix}

Then

\begin{matrix} (5) & \frac{δ L}{δ φ_{i σ}^{*} (r)} = 0 \end{matrix}

yields the Hartree-Fock equations

\begin{matrix} (6) & [\frac{p^{2}}{2 m} + u_{ext} (r) + v_{H} (r)] φ_{i σ} (r) + \int d r^{'} v_{X, σ} (r, r^{'}) φ_{i σ} (r^{'}) = ε_{i σ} φ_{i σ} (r) \end{matrix}

\begin{matrix} (7) & \begin{matrix} Hartree potential: & v_{H} (r) = \frac{e^{2}}{4 π ϵ_{0}} \int d^{3} r^{'} \frac{n (r^{'})}{| r - r^{'} |} \\ Exchange potential: & v_{x, σ} (r, r^{'}) = - \sum_{j \in occ} \frac{e^{2}}{4 π ϵ_{0} | r - r^{'} |} φ_{j σ}^{*} (r^{'}) φ_{j σ} (r) \end{matrix} \end{matrix}

$\Psi$ $\Psi'$ $N-1$ $\varphi_l$ . The Koopman shows

\begin{matrix} (8) & ⟨ Ψ | \hat{H} | Ψ ⟩ - ⟨ Ψ^{'} | \hat{H} | Ψ^{'} ⟩ = ε_{l} \end{matrix}

Single-hole excitation energy then is approximately

\begin{matrix} (9) & ε_{F} - ε_{l} \end{matrix}

Likewise for an unoccupied state, the single-particle excitation energy is approximately

\begin{matrix} (10) & ε_{l} - ε_{F} \end{matrix}

2. H-F approximation for the electron gas

Jellium model. A real crystal is complicated, with nuclei, core (inner shell) electrons and valence (outer shell) electrons. In the jellium model, retain only the valence electrons. The charge of ionic cores (离子实) is smeared into a neutralizing positive background without dynamics.

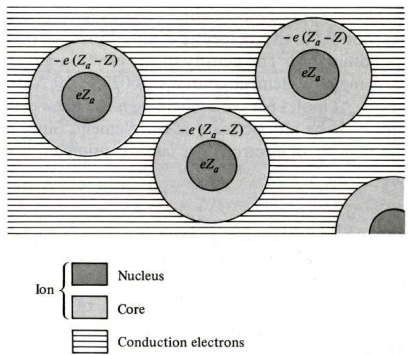
In this case, the Hartree potential gets cancelled out. Because of the translational invariance,

\begin{matrix} (11) & v_{X, σ} (r, r^{'}) = v_{X, σ} (r - r^{'}) \end{matrix}

ensuring planewave solutions. Then

\begin{matrix} (12) & ε_{k σ} = \frac{ℏ^{2} k^{2}}{2 m} + Σ (k) \end{matrix}

$\Sigma(\boldsymbol k)$ is the self energy (自能) of the Hartree-Fock approximation (the first two terms in the expansion below), which in this case has only exchange contribution.

Let's evaluate the self energy, which is the matrix element

\begin{matrix} \begin{aligned} \int d^{3} r \int d^{3} r^{'} φ_{k^{'} σ}^{*} (r) v_{X, σ} (r - r^{'}) φ_{k σ} (r^{'}) \\ = \frac{1}{V} \int d^{3} r \int d^{3} r^{'} e^{- i k^{'} \cdot r} v_{X, σ} (r - r^{'}) e^{i k \cdot r^{'}} \\ = δ_{k k^{'}} v_{X, σ} (k^{'}) \end{aligned} \end{matrix}

\begin{matrix} \begin{aligned} Σ (k) & = \frac{1}{V} \int d^{3} (r - r^{'}) e^{- i k \cdot (r - r^{'})} \sum_{j \in occ} v_{c} (r - r^{'}) \frac{1}{(2 π)^{3}} e^{i j \cdot (r - r^{'})} \\ = - \frac{1}{V} \sum_{j \in occ} v_{c} (k - j) \\ = - \int_{k^{'} < k_{F}} \frac{d^{3} j}{(2 π)^{3}} \frac{e^{2}}{ϵ_{0} | k - j |^{2}} \end{aligned} \end{matrix}

Finally, we have at the H-F level

\begin{matrix} (13) & Σ (k) = - \frac{e^{2} k_{F}}{2 π^{2} ϵ_{0}} [\frac{1}{2} + \frac{(1 - x^{2})}{4 x} \ln | \frac{1 + x}{1 - x} |] \end{matrix}

$x=k/k_\text F$ .

Note that on the Fermi surface

\begin{matrix} (14) & \begin{matrix} Σ (k_{F}) = - \frac{e^{2} k_{F}}{4 π^{2} ϵ_{0}} \\ {(\frac{d Σ}{d k})}_{k = k_{F}} = \infty \end{matrix} \end{matrix}

There is a Fermi surface, but the density of states at the Fermi level is zero!

\begin{matrix} g (ε) = \frac{2}{(2 π)^{3}} \int \frac{d S (ε)}{| \partial ε / \partial k |} \to 0 at ε_{F} \end{matrix}

The electron gas is incompressible within the H-F approximation.

What is missing? Screening, to be explained later.

3. Density functional theory 密度泛函理论

Density functional theory (DFT) is an exact many-body theory, based on two theorems of Hohenberg and Kohn.
With various local approximations, DFT offers a very powerful mean-field theory, using the Kohn-Sham equations
Hohenberg-Kohn theorems: density, instead of wavefunctions, as the key variable
Theorem 1: The g.s. of a many-electron system is a functional of density.
Theorem 2: The energy as a functional of the density is minimized by the g.s. density.
A many-electron system in an external potential coupling to density

\begin{matrix} (15) & \begin{matrix} H = \hat{T} + \hat{U} + {\hat{V}}_{ext} \\ {\hat{V}}_{ext} = \int d^{3} r v_{ext} (r) \hat{n} (r) \end{matrix} \end{matrix}

redutio ad absurdum $\Psi$ $\Psi'$ $v_{\text{ext}}$ $v_{\text{ext}}'$ , respectively. Suppose
$\begin{matrix} ⟨ Ψ | \hat{n} | Ψ ⟩ = ⟨ Ψ^{'} | \hat{n} | Ψ^{'} ⟩ \end{matrix}$
Then, by the Rayleigh-Ritz principle
$\begin{matrix} E^{'} = ⟨ Ψ^{'} | H^{'} | Ψ^{'} ⟩ < ⟨ Ψ | H^{'} | Ψ ⟩ = E + ⟨ Ψ | V^{'} - V | Ψ ⟩ \end{matrix}$
the inequality strictly holds. Similarly
$\begin{matrix} E < E^{'} + ⟨ Ψ^{'} | V - V^{'} | Ψ^{'} ⟩ \end{matrix}$
Adding the inequalities
$\begin{matrix} E + E^{'} < E^{'} + E \end{matrix}$
This cannot be true. Hence the supposition that two distinct g.s. have the same densities cannot be true.
- $\text{\"o}$ $v_{\text{ext}}\mapsto \Psi\mapsto n$ .
- $n\mapsto \Psi \mapsto v_{\text{ext}}$

$\Psi[n]$ , we may write
$\begin{matrix} (16) & \begin{matrix} E [n] = E_{int} [n] + \int d^{3} r v_{ext} (r) n (r) \\ E_{int} [n] = ⟨ Ψ | \hat{T} + \hat{U} | Ψ ⟩ \end{matrix} \end{matrix}$
$v_{\text{ext}}$ $n$ $n'$ $\Psi'$ .
$\begin{matrix} E [n^{'}] = E_{int} [n^{'}] + \int d^{3} r v_{ext} (r) n^{'} (r) = ⟨ Ψ^{'} | H | Ψ^{'} ⟩ > E [n] \end{matrix}$
The last inequality follows from the Rayleigh-Ritz principle.
$n$ $\Psi$ $v_{\text{ext}}$ $\Psi$ (not necessarily gs), then these densities are called N-representable.

4. Kohn-Sham equations

DFT as presented above is exact, elegant and useless.
Kohn and Sham proposed a set of equations to allow computation like the H-F approximation, called the Kohn-Sham equations.
The non-interacting v-representability. Suppose there is a fictitious (虚构的) non-interacting system
$\begin{matrix} (17) & {\hat{H}}_{s} = \hat{T} + {\hat{V}}_{s} \end{matrix}$
Then from the Hohenberg-Kohn theorem,
$\begin{matrix} (18) & E_{s} [n] = T_{s} [n] + \int d^{3} r v_{s} (r) n (r) \end{matrix}$
$T_s[n]$ $n_s$ $E_s[n]$ .
$v_s(\boldsymbol r)$ $n = n_s$
$\begin{matrix} (19) & n (r) = \sum_{i} f_{i} | φ_{i} (r) |^{2} \end{matrix}$
For the interacting system
$\begin{matrix} (20) & E [n] = T_{s} [n] + \int d^{3} r v_{ext} (r) n (r) + E_{H} [n] + E_{xc} [n] \end{matrix}$
where the exchange-correlation energy functional (交换关联泛函) is defined as

\begin{matrix} (21) & E_{xc} [n] = ⟨ Ψ [n] | \hat{T} + \hat{U} | Ψ [n] ⟩ - E_{H} [n] - T_{s} [n] \end{matrix}

$\delta E[n]=0$ . We introduce the Kohn-Sham Lagrangian
$\begin{matrix} (22) & L_{KS} = E [n] - \sum_{i} ε_{i} (⟨ φ_{i} | φ_{i} ⟩ - 1) \end{matrix}$
leading to the Kohn-Sham equations
$\begin{matrix} (23) & [\frac{p^{2}}{2 m} + v_{ext} (r) + v_{H} (r) + v_{xc} (r)] φ_{i} (r) = ε_{i} φ_{i} (r) \end{matrix}$
where the key novelty is exchange-correlation potential (交换关联势)
$\begin{matrix} (24) & v_{xc} (r) \equiv \frac{δ E_{xc}}{δ n (r)} \end{matrix}$
Kohn-Sham equations require self-consistent field solution like the H-F equations.
But the universal xc functional is unknown. To make this work, need approximations.
local-density approximation
$\begin{matrix} (25) & E_{xc} [n] ≃ \int d^{3} r n (r) ϵ_{xc} (n (r)) \equiv E_{xc}^{LDA} [n] \end{matrix}$
$\epsilon_{\mathrm{xc}}(n(\boldsymbol{r}))$ is the xc energy density of a uniform interacting electron gas and can be parametrized with higher-level quantum theory (like QMC).
Fixed-point iteration (self-consistent fields)
$\begin{matrix} (26) & n = KS [v [n]] \end{matrix}$