Lecture 5

Today

• Random-phase approximation

• Plasma oscillation, plasmon

• Fermi liquid theory

Reading

• GY 15.7-15.11.

1. The static Lindhard approximation

The polarization function is approximated as

Then

or

The density response is

where $v(q)$$v(q)$ is the screened potential

• response like a free electron via ${\chi }^0$$\chi^0$, but to the screened potential $v$$v$.

• sometimes called the self-consistent static Hartree (no exchange or correlation) approximation.

• Again, the screened potential displays Friedel oscillation

• This is missed in the Thomas-Fermi approximation.

2. Dynamical screening and random-phase approximation (RPA)

Including all the polarization in the free-electron gas

So the response function in the RPA is

Let's look at the expansion

diagrammatically, this looks like

If we take the expression for ${\chi }^0$$\chi^0$, and take the limit $q\to 0$$q\rightarrow 0$ with $\omega$$\omega$ being finite

This is the so-called dynamical limit.

The dielectric function in the RPA is

• new poles at $q=0$$q=0$ at frequency ${\mathrm{\Omega }}_{\text{p}}$$\Omega_{\text p}$, corresponding to the classical plasma oscillation.

• Support density oscillation even in the absence of external drive, by virtue of intrinsic excitation of the system.

• The fact that these modes show up as poles in $\chi$$\chi$ means the particle-hole excitation picture does not work in this case. In fact, plasma oscillation （等离子振荡）is an example of the collective excitations (集体激发).

Plasma oscillation, arising from the instability of the density response function, is the uniform density oscillation in a conducting media. The absence of $\hslash$$\hbar$ in the expression for ${\mathrm{\Omega }}_{\text{p}}$$\Omega_{\text p}$ suggests that this is of a classical origin. Now we try to give a classical derivation. Suppose that the electron gas is displaced by $u$$u$, which gives rise to a polarization

Then the depolarization field is $E_d=neu/{ϵ}_0$$E_d= neu/\epsilon_0$, so that the equation of motion is

so, ${\mathrm{\Omega }}_{\text{p}}$$\Omega_{\text p}$ the resonance frequency at which the electron gas supports a uniform oscillation.

From $\text{(8)}$$\eqref{eq:chirpa}$, we have the small $q$$q$ expansion

In order for the dielectric function to vanish, we require

Solving for ${\omega }^2\to {\mathrm{\Omega }}_{\text{p}}(q{)}^2$$\omega^2 \rightarrow \Omega_{\text p}(q)^2$

• quadratic dispersion for small $q$$q$, with a gap ${\mathrm{\Omega }}_{\text{p}}$$\Omega_{\text p}$.

• The appearance of $v_{\text{F}}$$v_\text F$: plasmon $(q\ne 0)$$(q\neq 0)$ is a quantum mechanical result.

• A plasmon is a quantum of plasma oscillation.

• Significant broadening inside the e-h continuum: damping (阻尼).

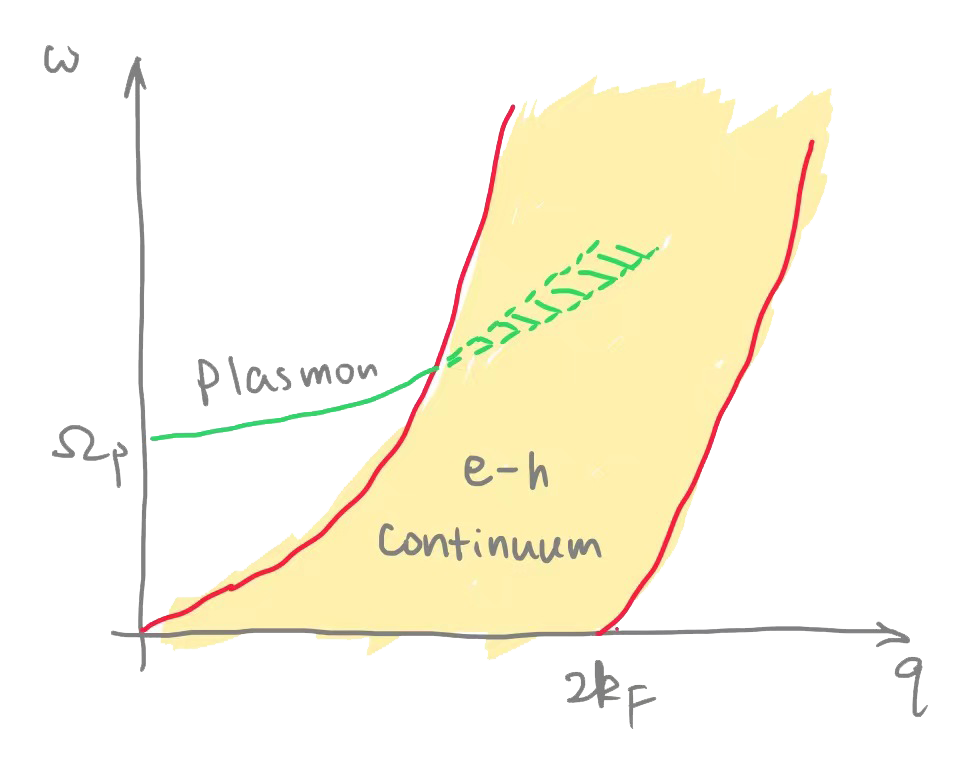
[I will leave 15.10 Optical properties for self study.]

3. Landau Fermi liquid theory

The $r_s$$r_s$ for electrons in typical metals are neither small nor large. This means that the interaction is quite strong. But as we study the band structure of crystals, we pretend there is no interaction at all. And many results are very successful. Why?

The success of these free-fermion theories is rooted in the Landau's liquid theory, which is based on the assumption of an adiabatic connection between the fully interacting electron liquid and the free fermion limit.

4. Elementary excitations

In the grand canonical ensemble (巨正则系综), the grand Hamiltonian is written

where $\mu$$\mu$ is the chemical potential, and $N$$N$ the particle number. If the Hamiltonian $H$$H$ conserves particle number, $N$$N$ may be replaced by its (mean) value.

For a non-interacting electron gas then

In the ground state, $n_{\mathit{k}s}^{(0)}=1$$n_{\boldsymbol ks}^{(0)}=1$ if ${\epsilon }_{\mathit{k}s}<0$$\varepsilon_{\boldsymbol ks}<0$, and $n_{\mathit{k}s}^{(0)}=0$$n_{\boldsymbol ks}^{(0)}=0$ if ${\epsilon }_{\mathit{k}s}>0$$\varepsilon_{\boldsymbol ks}>0$.

What can happen to the gas? It can be dislodged into an excited state by

For an occupied state (占据态) ($k<k_{\text{F}}$$k<k_\text F$), ${\delta }_{\mathit{k}s}=0,-1$$\delta_{\boldsymbol ks}= 0, -1$; for an unoccupied state (非占据态) ($k>k_{\text{F}}$$k>k_\text F$), ${\delta }_{\mathit{k}s}=0,+1$$\delta_{\boldsymbol ks}= 0, +1$.

• a single particle excitation (单粒子激发) : occupancy (占据) one state is changed

• single-electron excitation outside the Fermi sea

• single-hole excitation inside the Fermi sea

• In both cases, the energy of excitation is

• Near the Fermi energy, we can make the linear expansion

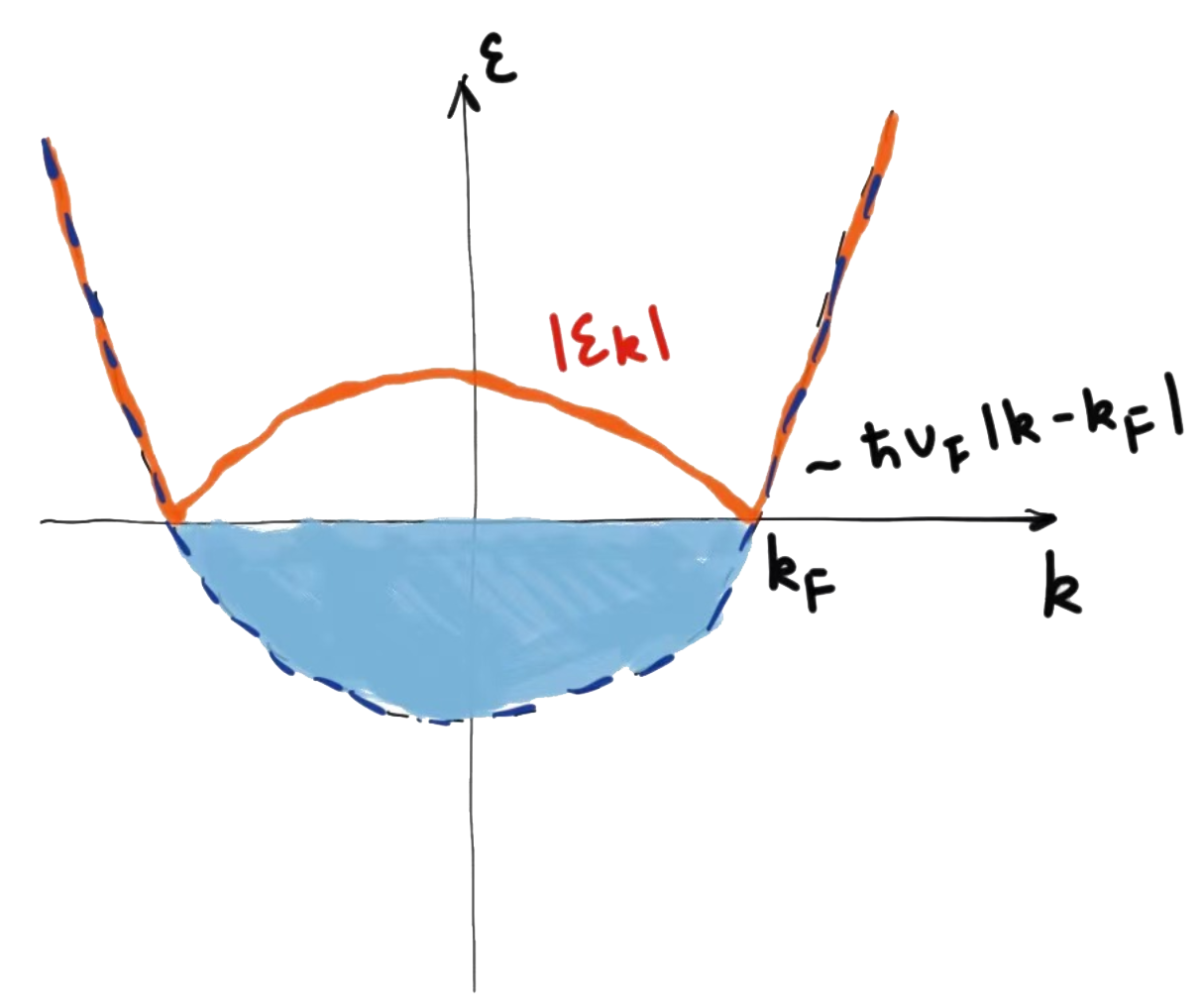
• A single-hole or a single hole excitation is called an elementary excitation.

• An elementary excitation (元激发) has well-defined energy, momentum and dispersion relation (色散关系), and all excited states of the system can be built from elementary excitations.

• So an elementary excitation in this case changes the total particle number. This is why we use grand canonical ensemble.

• The simplest excitation in a canonical ensemble (正则系综) is the electron-hole pair excitation, which is not elementary because there is no well-defined dispersion relation (色散关系) as seen from the e-h continuum, and because not all excited states can be built from e-h pairs.

5. Adiabatic connection and quasiparticle concept

The free-fermion system can be solved easily, thanks to the fact that it has a lot of constants of motion: $N$$N$ as well as all the $n_{\mathit{k}s}$$n_{\boldsymbol ks}$'s. This follows from $[K_0,n_{\mathit{k}s}]=0$$[K_0,n_{\boldsymbol ks}]=0$, so that there are many independent $U(1)$$U(1)$ symmetries.

This existence of a huge number of symmetries is not generic. Interaction usually breaks it, $[U,n_{\mathit{k}s}]\ne 0$$[U,n_{\boldsymbol ks}]\neq 0$. This is responsible for the fact that most interacting problems are not exactly solvable.

Let's introduce the interaction to a free-fermion system slowly or adiabatically, with a tuning parameter $\lambda \in [0,1]$$\lambda\in[0,1]$

Adiabatic connection is assumed. For $\lambda =0$$\lambda =0$, the electron gas ground state is non-degenerate. As long as the system stays this way for $0<\lambda \le 1$$0<\lambda\le 1$, we non-interacting electron gas is adiabatically connected to the interacting ground state. In other words, there is no phase transition between $\lambda =0$$\lambda=0$ and $\lambda =1$$\lambda =1$, so the change is an analytic function (no singularity).

Such a singularity would signal an instability of the ground state and should be viewed as a phase transition. Thus, if there are no phase transitions, there should be a smooth connection between noninteracting and interacting ground states.

What about the excited states?

• Now consider a single particle excitation at $k_0>k_{\text{F}}$$k_0>k_\text F$: $\delta n_{{\mathit{k}}_{0}s}=+1$$\delta n_{\boldsymbol k_0 s}=+1$. Without interaction, the particle will stay forever.¹

• With interaction, however, this particle can scatter with other particles.

• For example, ${\mathit{k}}_0\to {\mathit{k}}_1$$\boldsymbol k_0 \rightarrow \boldsymbol k_1$, with the production of a pair of hole $k_2<k_{\text{F}}$$k_2<k_\text F$, and particle $k_3>k_{\text{F}}$$k_3>k_\text F$. See the figure below.

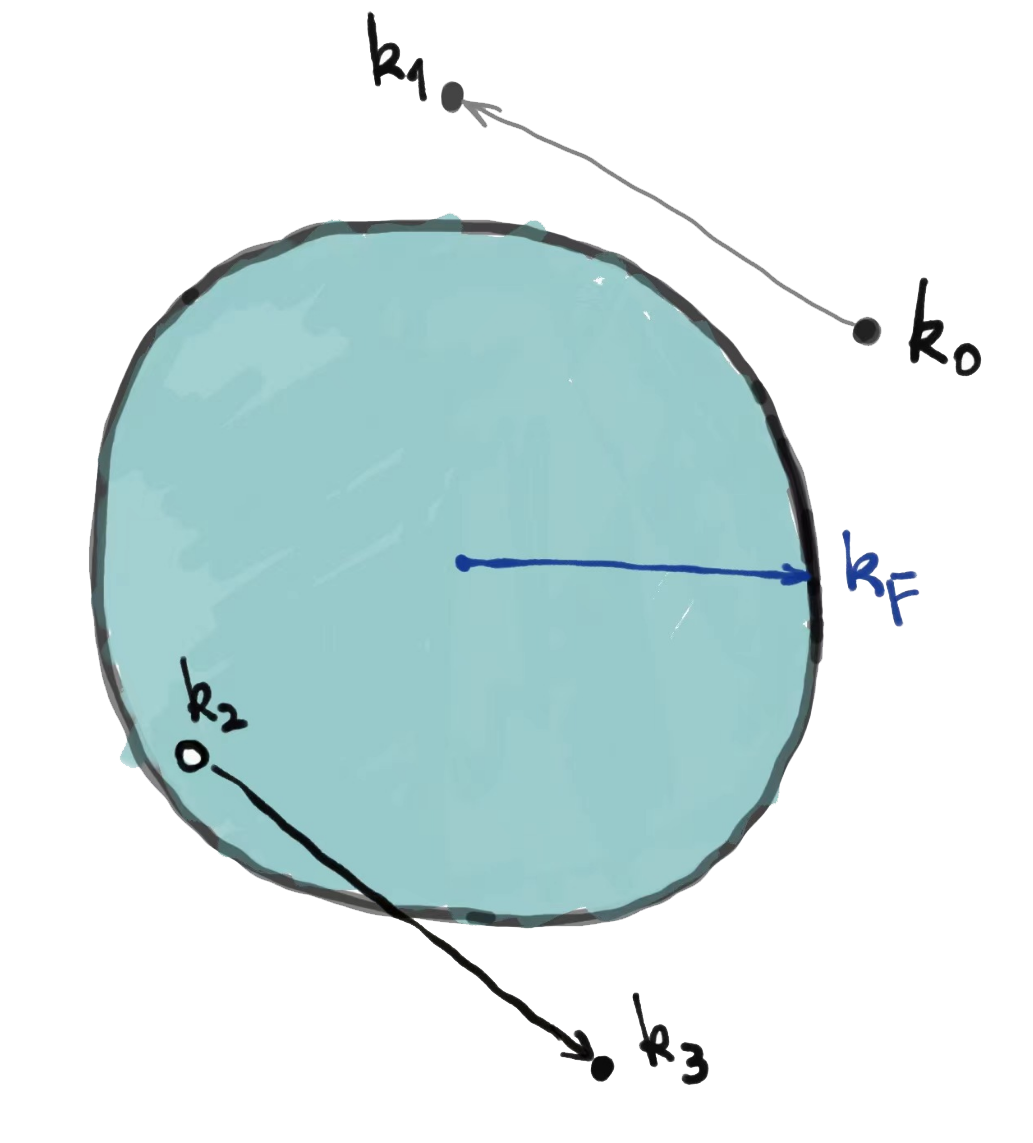
• One can always find ${\mathit{k}}_1,{\mathit{k}}_2,{\mathit{k}}_3$$\boldsymbol{k}_1, \boldsymbol{k}_2,\boldsymbol{k}_3$ (possibly many combinations) to satisfy the momentum and energy conservation

• Scattering is inevitable and all these excited states mix.

• To identify the interacting excited states with the non-interacting excited states seems hopeless.

Landau argued that although adiabaticity cannot be established for every excited state, it may be established for low-energy excited states at least approximately. The kinematic (动理学) consideration in $\text{(24)}$$\eqref{eq:consv}$ implies ${\epsilon }_{{\mathit{k}}_1},|{\epsilon }_{{\mathit{k}}_2}|,{\epsilon }_{{\mathit{k}}_3}<{\epsilon }_{{\mathit{k}}_0}$$\varepsilon_{\boldsymbol k_1}, |\varepsilon_{\boldsymbol k_2}|, \varepsilon_{\boldsymbol k_3} < \varepsilon_{\boldsymbol k_0}$. Then for a low-energy electron excitation,

we have

This means,

In other words, the phase space (相空间) for the scattering is restricted to a very thin shell close to the Fermi surface, with a thickness $\delta k_0$$\delta k_0$. From the Fermi's Golden rule, the scattering rate is

That's is, for sufficiently low-energy excitations, $\delta k_0\to 0$$\delta k_0\rightarrow 0$, the excitation can be arbitrarily (任意地) long-lived. In other words, low-energy excitations are not efficiently scattered due to the kinematic constraint. In fact,²

Then these low-lying single-particle excitations can be good approximations of the exact eigenstates of $K(1)$$K(1)$. There is an approximate one-to-one correspondence between the non-interacting and interacting excitations, which is asymptotically exact at zero energies.

Thus $n_{\mathit{k}s}$$n_{\boldsymbol k s}$ are approximately good quantum numbers for sufficiently low energies and temperatures. The room temperature is about $1/40$$1/40$ of an eV, much lower than typical Fermi energy, and can be considered a "low temperature". These low-lying long-lived excitations are called quasiparticles (准粒子).

References and notes