Lecture 06

Today

• Landau energy functional

• Properties of a Fermi liquid

• Instabilities

1. Landau's Fermi liquid

Then one can hope to describe all possible change from the ground state by enumerating $\delta n_{\mathit{k}s}$$\delta n_{\boldsymbol k s}$. This motivates the Landau's energy functional

Definition:

$v_{\text{F}}^{\ast }$$v_{\text F}^*$ is the Fermi velocity renormalized (重整化的) by the interaction, which is often parametrized by an renormalized effective mass (有效质量)

Note that $m$$m$ is band mass,[^1] not the rest mass of an electron.

The Landau's $f$$f$-function is defined as

The $f$$f$-function can be simplified by symmetry. Since $k,k^{\prime }$$k,k'$ are close to $k_{\text{F}}$$k_\text F$, we will consider their angular dependence. Rotational invariance of the system means

where $\cos \theta =\hat{\mathit{k}}\cdot {\hat{\mathit{k}}}^{\prime }$$\cos \theta = \hat{\boldsymbol k} \cdot \hat{\boldsymbol k}'$

Spin rotational invariance means

so we use the symmetric and antisymmetric (发对称的) combinations

• $f^{\text{s}}\to$$f^\text s\rightarrow$ charge, $f^{\text{a}}\to$$f^\text a\rightarrow$ spin

Since $f$$f$ has the units of energy, we combine it with the density of states to give a dimensionless quantity

where by virtue of the Luttinger theorem ($k_{\text{F}}$$k_\text F$ is not changed by interaction)

So the expansion is written[^2]

2. Physical properties of Fermi liquids

For a theory to be useful, it must lead to experimentally measurable quantities. It is clear that the theory applies when $k_{B}T\ll \mu$$k_BT\ll \mu$ and the quantities of interest involve mostly low-energy excitations.

• Isochoric heat capacity $C_V$$C_V$

  Let's first compute the heat capacity for fixed volume $V$$V$ and particle number $N$$N$

  $$\begin{array}{}\text{(11)}& C_V=\frac{\partial ⟨E⟩}{\partial T}\end{array}$$

  Using the Sommeld expansion[^2]

  $$\begin{array}{}\text{(12)}& ⟨E⟩=2\int \text{d}\epsilon \epsilon g(\epsilon )f^0(\epsilon )\approx E_0+2\times \frac{{\pi }^2}{6}(k_{B}T{)}^{2}g(0)\end{array}$$

  So the heat capacity is

  $$\begin{array}{}\text{(13)}& C_V=\frac{2{\pi }^2}{3}g(0)k_B^{2}T.\end{array}$$

  This is like the free electron result, except that the density of states has been renormalized by the interaction

  $$\begin{array}{}\text{(14)}& g(0)\sim \frac{1}{v_{\text{F}}^{\ast }}\sim m^{\ast }\end{array}$$

  so

  $$\begin{array}{}\text{(15)}& C_V(T)=\frac{m^{\ast }}{m}{C}_V^0(T).\end{array}$$

  Measuring the heat capacity will give us information about $m^{\ast }$$m^*$.

  Why drop the interaction term in Landau functional? Observe

  $$\begin{array}{}\text{(16)}& \delta N=\sum _{\mathit{k},s}\delta n_{\mathit{k}s}=0\end{array}$$

  s.t.

  $$\begin{array}{}\text{(17)}& \begin{array}{rl}⟨\sum _{\mathit{k},s,{\mathit{k}}^{\prime },s^{\prime }}{f}_{\mathit{k},s,{\mathit{k}}^{\prime },s^{\prime }}\delta n_{\mathit{k},s}\delta n_{{\mathit{k}}^{\prime },s^{\prime }}⟩& \approx \sum _{\mathit{k},s,{\mathit{k}}^{\prime },s^{\prime }}{f}_{\mathit{k},s,{\mathit{k}}^{\prime },s^{\prime }}⟨\delta n_{\mathit{k},s}⟩⟨\delta n_{{\mathit{k}}^{\prime },s^{\prime }}⟩\\ & =(\delta N{)}^2\bar{f}\end{array}\end{array}$$

  the last line is obtained by separating the summation into $k,k^{\prime }$$k,k'$ and $\hat{k},{\hat{k}}^{\prime }$$\hat k,\hat k'$.

  Beyond the mean field,

  $$\begin{array}{}\text{(18)}& \sum _{\mathit{k},s,{\mathit{k}}^{\prime },s^{\prime }}{f}_{\mathit{k}s,{\mathit{k}}^{\prime }{s}^{\prime }}⟨(\delta n_{\mathit{k}s}-⟨\delta n_{\mathit{k}s}⟩)(\delta n_{{\mathit{k}}^{\prime }{s}^{\prime }}-⟨\delta n_{{\mathit{k}}^{\prime }{s}^{\prime }}⟩)⟩\end{array}$$

  this correlation contribution can also be dropped if $f_{\mathit{k}s,{\mathit{k}}^{\prime }{s}^{\prime }}$$f_{\boldsymbol{k}s, \boldsymbol{k}^{\prime} s^{\prime}}$ is a slowly varying function.

   

• Isothermal compressibility $\kappa$$\kappa$

  $$\begin{array}{}\text{(19)}& \kappa =-{\frac{1}{V}\frac{\partial V}{\partial P}|}_{T,N}=\frac{1}{n^2}\frac{\partial n}{\partial \mu }\end{array}$$

  from the Gibbs-Duhem relation

  $$\begin{array}{}\text{(20)}& N\text{d}\mu =-S\text{d}T+V\text{d}p\end{array}$$

  which comes from the fact that $\mu$$\mu$ is the partial molar (偏摩尔) Gibbs free energy.

  So at $T=0$$T=0$

  $$\begin{array}{}\text{(21)}& {\kappa }^0=\frac{2g^0(0)}{n^2}\end{array}$$

  So there is factor from change in the density of state, by the factor $m^{\ast }/m$$m^*/m$.

  Now we need consider the effect of interaction on $\mu$$\mu$. putting additional electrons on the Fermi sea expands the Fermi surface, there is an additional change in the chemical potential from the interaction:

  $$\begin{array}{}& \begin{array}{c}\begin{array}{rl}\delta \mu & =\hslash v_{\mathrm{F}}^{\ast }\delta k_{\mathrm{F}}+\sum _{{\mathit{k}}^{\prime },s^{\prime }}{f}_{\mathit{k}s,{\mathit{k}}^{\prime }{s}^{\prime }}\delta n_{{\mathit{k}}^{\prime }{s}^{\prime }}\\ & =\delta k_{\mathrm{F}}(\hslash v_{\mathrm{F}}^{\ast }+2\sum _{{\mathit{k}}^{\prime }}{f}_{\hat{k}{\hat{k}}^{\prime }}^{\text{s}}\frac{\partial n_{{\mathit{k}}^{\prime }{s}^{\prime }}}{\partial k_F})\\ & =\hslash v_{\mathrm{F}}^{\ast }\delta k_{\text{F}}[1+2\sum _{{\mathit{k}}^{\prime }}\delta ({\epsilon }_{k^{\prime }})\int \frac{\text{d}\mathrm{\Omega }}{\mathrm{\Omega }}{f}^{\text{s}}(\theta )]\\ & =\hslash v_{\mathrm{F}}^{\ast }\delta k_{\text{F}}(1+F_0^{\text{s}})\end{array}\end{array}\end{array}$$

  Notice that

  $$\begin{array}{}& \frac{\partial \mu }{\partial n}=\frac{\partial \mu /\partial k_{\text{F}}}{\partial n/\partial k_{\text{F}}}\end{array}$$

  And the quantity $\partial n/\partial k_{\text{F}}=k_{\text{F}}^2/{\pi }^2$$\partial n/\partial k_\text F= k_\text F^2/\pi^2$ is not affected by interaction, per the Luttinger theorem.

  The renormalized compressibility is

  $$\begin{array}{}\text{(22)}& \kappa ={\kappa }^0\frac{m^{\ast }/m}{1+F_0^{\text{s}}}\end{array}$$

  So measuring the compressibility leads to $F_0^{\text{s}}$$F_0^\text s$.

  

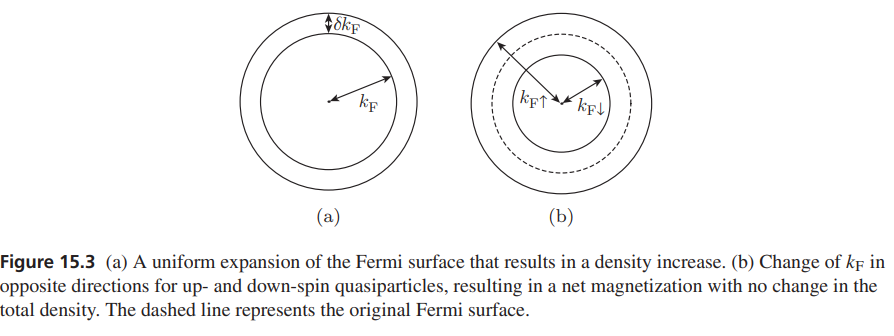
• Spin susceptibility ${\chi }_{\text{S}}$$\chi_\text S$

  $$\begin{array}{}\text{(23)}& {\chi }_{\mathrm{s}}={\chi }_{\mathrm{s}}^0\frac{m^{\ast }/m}{1+F_0^{\mathrm{a}}}\end{array}$$

• Collective excitations, transport properties.

3. Fermi liquid instability

• FL theory based on adiabatic connection to the free fermion gs.

• there can be new gs when the interaction is turned on, arising from Fermi-liquid

• Symmetry may be spontaneously (自发地) broken in the phase transition (相变)

• Ferromagnetic instability: $F_0^{\text{a}}=-1$$F ^\text a_0=-1$

  • divergence of ${\chi }_{\text{S}}$$\chi_\text S$ signals instability

  • Let the energy of a non-magnetic system be

    $$\begin{array}{}\text{(24)}& E(M)=E_0+\frac{1}{2}\alpha M^2\end{array}$$

    where $\alpha$$\alpha$ is the stiffness.

    Now we apply an external field coupled linear with $M$$M$

    $$\begin{array}{}\text{(25)}& E(M,B)=E_0+\frac{\alpha }{2}{M}^2+B\cdot M\end{array}$$

    Then $M$$M$ is going to attain an equilibrium value

    $$\begin{array}{}\text{(26)}& M_{\text{eq}}=-\frac{B}{\alpha }.\end{array}$$
    $$\begin{array}{}\text{(27)}& E(M_{eq})=E_0-\frac{B^2}{2\alpha }\end{array}$$

    we see

    $$\begin{array}{}\text{(28)}& {\chi }_S=-\frac{1}{\alpha }\end{array}$$

    So, ${\chi }_S\to \mathrm{\infty }$$\chi_S\rightarrow \infty$ means $\alpha \to 0$$\alpha \rightarrow 0$. higher order term sets in

    

   

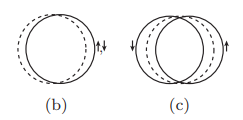
• Pomerrachuk instability: deformation of Fermi surface, when $F<-1$$F<-1$

  • Ferromagnetic: FS enlarges for one spin, shrinks for the other.

  • nematic Fermi liquid: $F_2^{\text{s}}<-1$$F_2^\text s<-1$

    

    

   

• Pairing instability: two quasiparticles

  completely local interaction: $V_{k{k}^{\prime }}=V_0$$V_{kk'}= V_0$.

  consider a singlet pair: $|k⟩=|k\uparrow ,-k\downarrow ⟩$$|k\rangle=|k\uparrow,-k\downarrow\rangle$.

  For the Fermi liquid Hamiltonian $H_0$$H_0$

  $$\begin{array}{}\text{(29)}& \begin{array}{rl}{\hat{H}}_0|\mathit{k}⟩& =2{ϵ}_{\mathit{k}}|\mathit{k}⟩,\\ ⟨{\mathit{k}}^{\prime }|\hat{V}|\mathit{k}⟩& =V_{\mathit{k}{\mathit{k}}^{\prime }}=V_0.\end{array}\end{array}$$

  Since QP are well defined near the Fermi surface, we introduce a cutoff

  $$\begin{array}{}\text{(30)}& 0<{\epsilon }_k<E_{\text{c}}=\hslash v_{\text{F}}^{\ast }{k}_{\text{c}}\end{array}$$

  This two-body problem is exactly solvable, and the solution is non-perturbative, because there is a discontinuity at $V_0=0$$V_0=0$.

  We will do a perturbative RG. Starting at an arbitrary cutoff energy $\mathrm{\Lambda }<E_c$$\Lambda < E_c$

  

  $$\begin{array}{}\text{(31)}& \begin{array}{rl}V(\mathrm{\Lambda }-d\mathrm{\Lambda })& =V(\mathrm{\Lambda })+\sum _{\mathrm{\Lambda }-d\mathrm{\Lambda }<{ϵ}_{{\overrightarrow{k}}^{\prime \prime }}<\mathrm{\Lambda }}\frac{V^2(\mathrm{\Lambda })}{-2\mathrm{\Lambda }}\\ & =V(\mathrm{\Lambda })-\frac{g(0)V^2(\mathrm{\Lambda })}{2}\frac{d\mathrm{\Lambda }}{\mathrm{\Lambda }},\end{array}\end{array}$$

  We find a RG flow equation

  $$\begin{array}{}\text{(32)}& \frac{dV(\mathrm{\Lambda })}{d\log \left(E_{\mathrm{c}}/\mathrm{\Lambda }\right)}=-\frac{g(0)V^2(\mathrm{\Lambda })}{2}.\end{array}$$

  

  • RG: repulsive interaction is irrelevant, attraction is relevant

  Integrating the RG equation

  $$\begin{array}{}\text{(33)}& V(\mathrm{\Lambda })=\frac{V_0}{1+(g(0)V_0/2)\ln \left(E_{\mathrm{c}}/\mathrm{\Lambda }\right)}\end{array}$$

  • If $V_0>0$$V_0>0$, the interaction renormalizes to zero

  • If $V_0<0$$V_0<0$, the interaction diverges at

    $$\begin{array}{}\text{(34)}& {\mathrm{\Lambda }}_c=E_c{e}^{-2/g(0)|V_0|}\end{array}$$

    That is, the RG breaks down at we get close the FS, because new physics shows up: a bound state!

  • Cooper problem: Cooper pair

• New physics: a pair of electrons on a Fermi sea are unstable against attractive interactions, however weak they may be. This is unlike in the free space, where only finite attraction leads to bound state.

• Cooper pair: from the wave function in (15.179), the orbital part of the wavefunction is symmetric under exchange. so the spin part is antisymmetric singlet.

• s-wave: The wavefunction has no angular dependence.

• The formation of the novel bound states does not stop at two particle level. When a lot of bound pairs form and condense, the FS is destroyed: gapped condensate: superfluid or superconductor.

References and notes

[1] Band mass is the effective mass in the band theory.

[2] We can expand expand any piecewise continuous function in terms of the Legendre (勒让德) polynomial

with

[3] The Sommerfeld expansion is especially useful when evaluating an integral of the form:

In a low-temperature expansion, we find

where the coefficient $a_n$$a_n$ is related to the Riemann zeta function $\zeta (k)$$\zeta(k)$, as

Usually, we truncate the expansion at $n=1$$n=1$, with $a_1={\pi }^2/6$$a_1= \pi^2/6$, so