Lecture 7
Today
Charge and magnetic impurity in Fermi liquid
Wavepacket dynamics
Semiclassical dynamics (general)
Infrared singularities: some additional interesting features of the low-energy physics of the electron gas associated with the gapless spectrum of the Landau Fermi liquid and the finite density of states for low-energy excitations.
"In physics, an infrared divergence (also IR divergence or infrared catastrophe) is a situation in which an integral, for example a Feynman diagram, diverges because of contributions of objects with very small energy approaching zero, or equivalently, because of physical phenomena at very long distances."
The neutralization of the impurity charge requires electron flow from infinite distances. This means that the ground state with the impurity is orthogonal to that without, a fact called the e infrared or orthogonality “catastrophe”.
Suddenly turn on the impurity. The weight of new gs is zero. the dynamics is characterized by creating low-energy excitations in the electron gas
Energy dumped into the e-h pairs is finite, but the number is infinite. Hence the name infrared divergence or catastrophe.
1. Friedel sum rule
From the static Lindhard approximation
Now we put a test point charge
that is, the screening charge completely neutralizes the external charge.
In the Fermi liquid approach, we treat the particles as nearly non-interacting.
Asymptotic wavefunction are spherical waves, for the angular momentum channel
need to count the density of states, within a certain large radius
choosing a boundary condition
total number of states below energy
The 1st term is number of states without impurity
The change in number of states
Since the bulk value of the Fermi energy is not shifted by the presence in the system of a single impurity, we can replace K by the Fermi wave vector
Friedel sum rule:
The factor
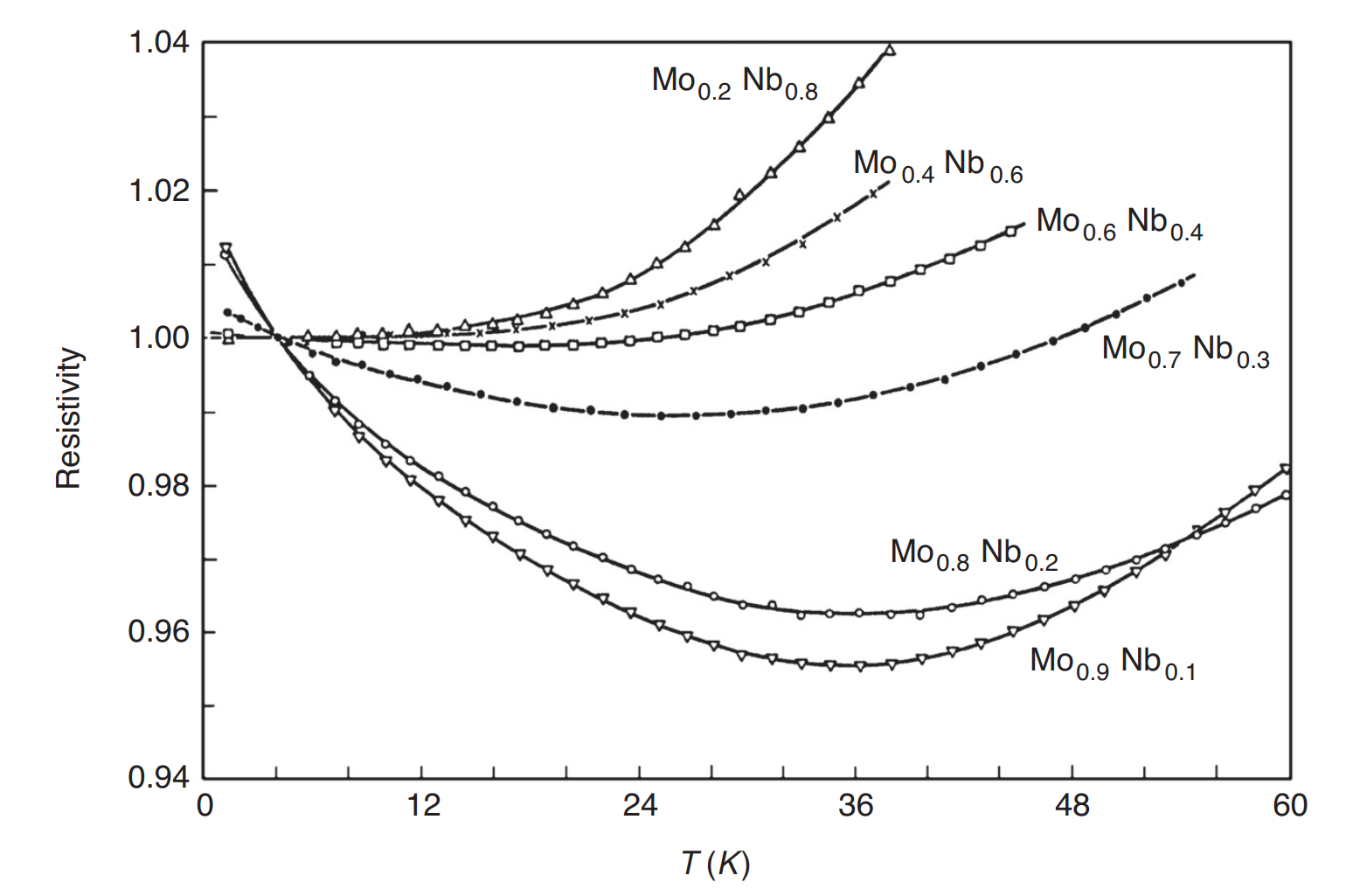
2. Kondo problem
Dilute magnetic impurity in metals
The essence of the problem is the exchange coupling of a local spin with the Fermi surface
where, with
isotropic exchange:
anisotropy:
We begin with a simpler problem
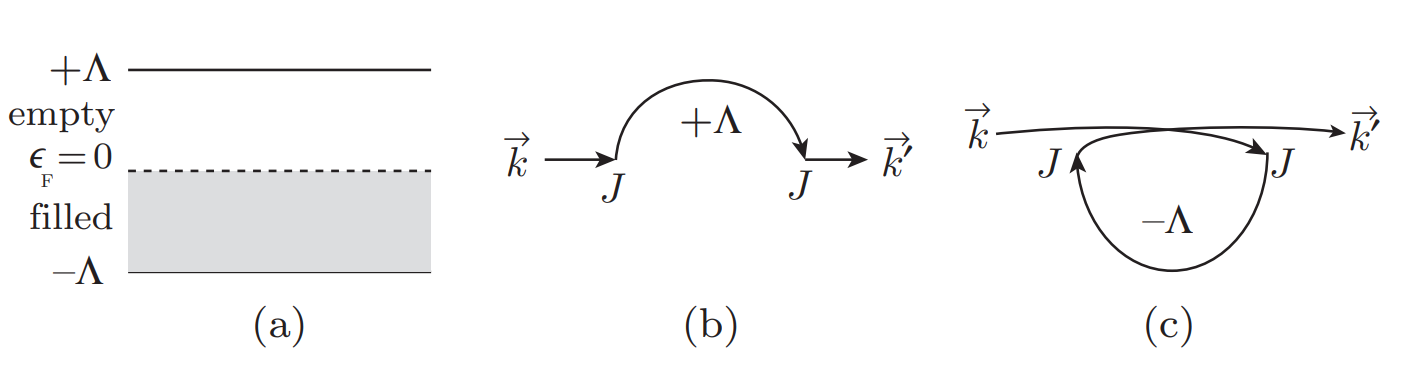
particle route (b)
where
hole route (c)
So the flow equation is marginal
Now we renormalize the exchange interaction.
If
But when
For the particle write for
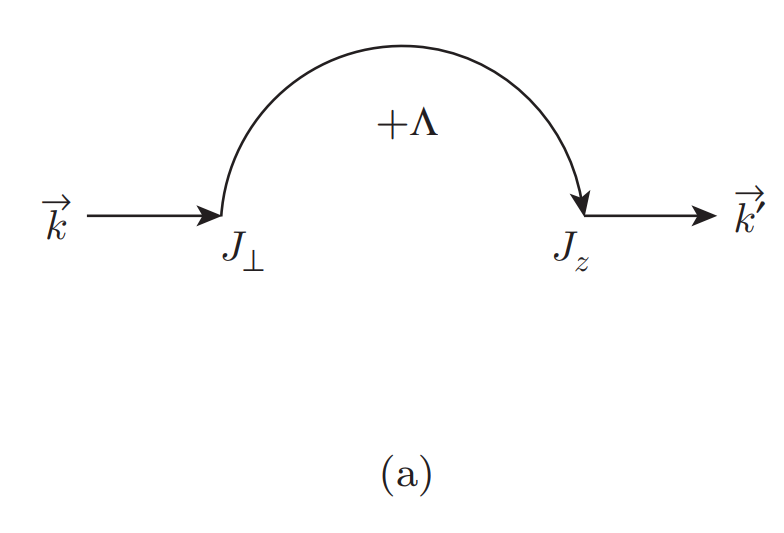
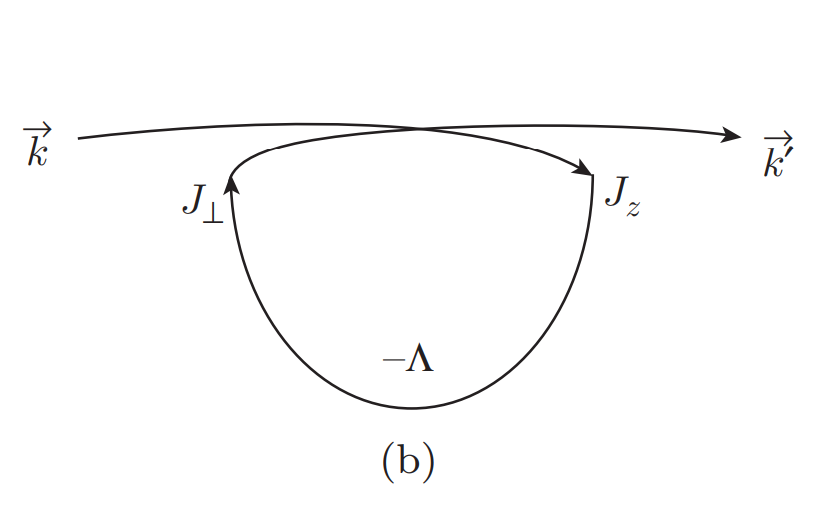
So the flow equation
Invariant of the flow
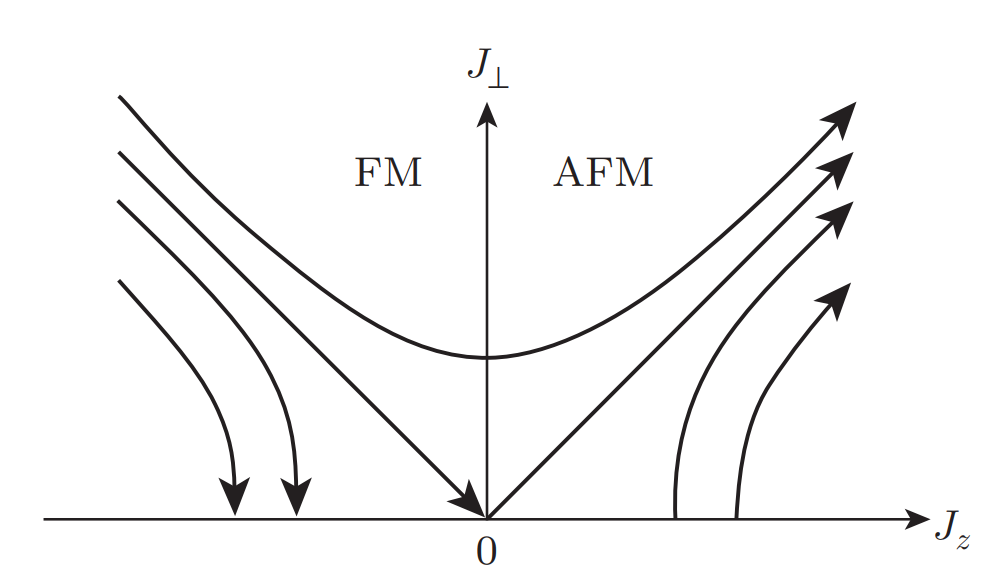
Ferromagnetic case:
Antiferromagnetic coupling is relevant. quenches the Curie susceptibility, and contributes to the electrical conductance.
Finite temperatures:
divergence at the Kondo temperature
In a static H-F approximation,

Kenneth Wilson’s non-perturbative numerical treatment of the flow equations (including the flow of many new coupling constants associated with new terms generated in the Hamiltonian) gives quantitatively accurate results valid down to arbitrarily low temperatures [134]. Quite remarkably, Nathan Andrei [135, 136] and Paul Wiegman [137] were later able to provide exact analytic expressions for the many-body eigenstate wave functions using Bethe ansatz methods.
3. Wavepacket in free space (1D)

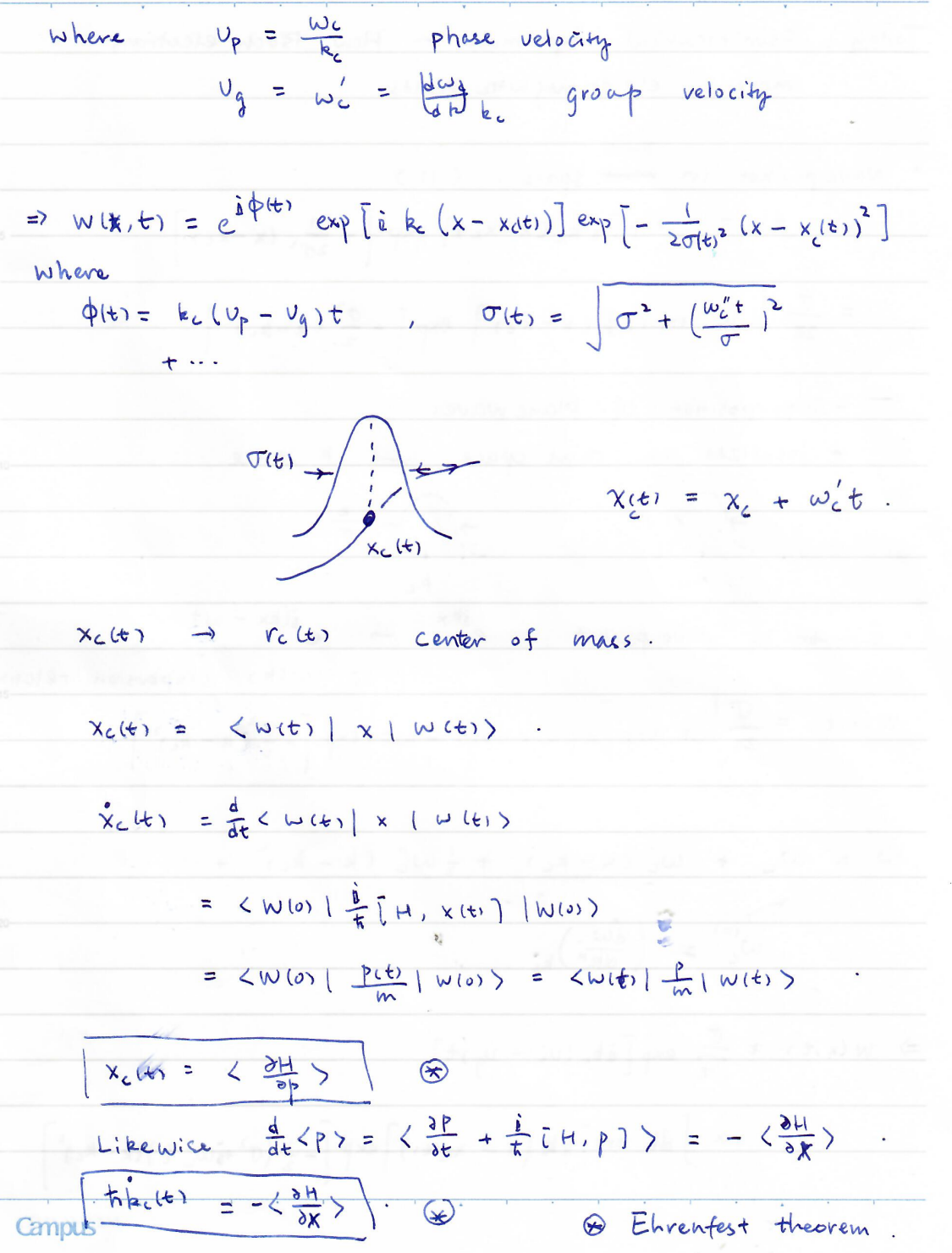


4. Semiclassical dynamics
The time-dependent variational principle
the variation of which leads to the td Sch
Now we develop a generalized variational principle
The Lagrangian is then
where
The action
The Euler-Lagrange equation of motion is
Or
where
We note that it is not accidental (偶然的) that
Consider an infinitesimal interval of time
The phase space volume
where the Jacobian matrix is
To find the determinant of
We find
Trivial case:
phase space density is constant. This is the Liouville theorem.
Generally, the dynamics has nontrivial geometry, and we now have the generalized Liouville theorem for Eq.
Transforming back to
So we have
The genialized Liouville theorem
Reference and notes
[1] Since
So we can choose
which turns out to be real-valued.