Lecture 8
1. Wavepacket
In free-space (1D), the wavepacket (波包) at
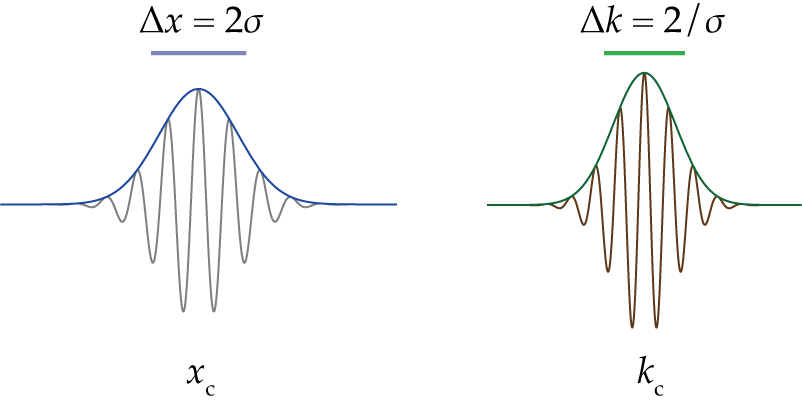
The packet evolves as
where
we find
where
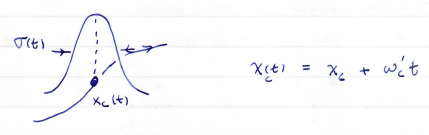
So
This is the so-called Ehrenfest theorem.
That is to say, if we talk about a wavepacket in terms of its center of mass and center of momentum, we may recover the classical dynamics. This is the key idea of semiclassical dynamics.
We want to apply this trick to Bloch electrons, so we need wavepacket that is localized in both real and k-space
Normalization
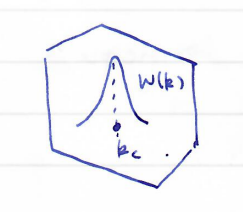
center of mass:
center of momentum:
What is
In the last step, we have performed an integration by parts (分部积分). We now introduce a quantity call the Berry connection
So the center of the wavepacket is
that is simply stating that in the Bloch representation
The Bloch wavefunctions have
is still the same Bloch state. Under this change of basis, we find
which ensures that the center of a wavepacket is invariant.
2. Semiclassical equations of motion
In an external electromagnetic potential
After a careful calculation1
where
Hereafter, we will drop subscript
For a uniform magnetic field,
So this leads to the EOM
The novel term in the Lagrangian is
where the pseudovector
3. Anomalous Hall effect
Under an electric field, the anomalous velocity can cause a transverse current, even without an external magnetic field. This is called the anomalous Hall effect (反常霍尔效应).
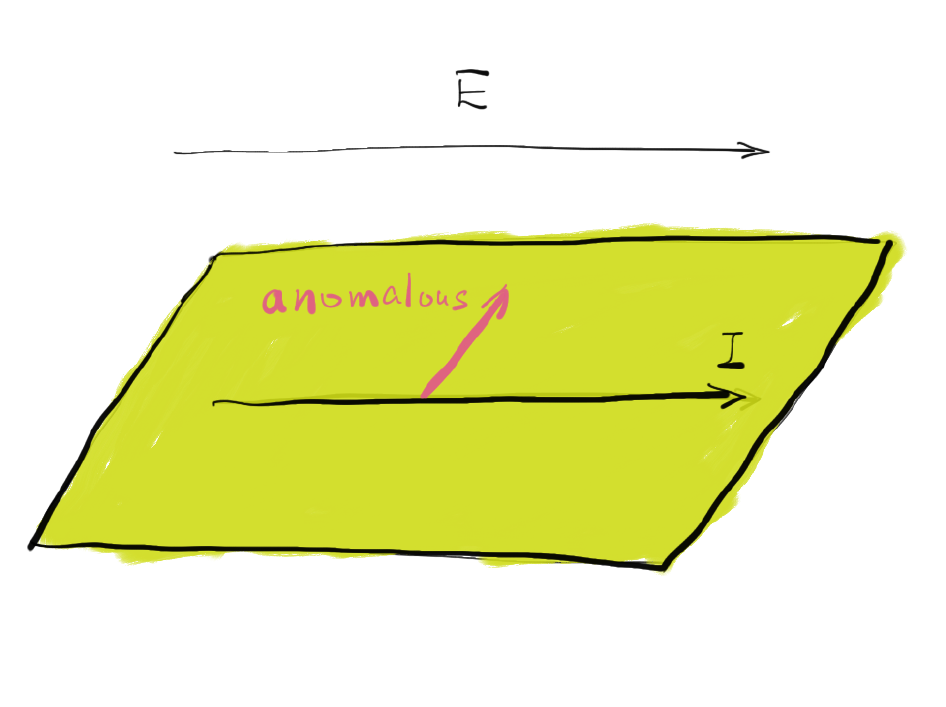
Historically, there had been an debate over the origin of the anomalous Hall effect (AHE). If the anomalous Hall current comes from the Berry curvature of the Bloch bands, as described above, it is called the intrinsic AHE since it depends on the band structure and not on scattering. Correspondingly, the AHE conducitivtiy is
Take a two-dimensional system as an example,
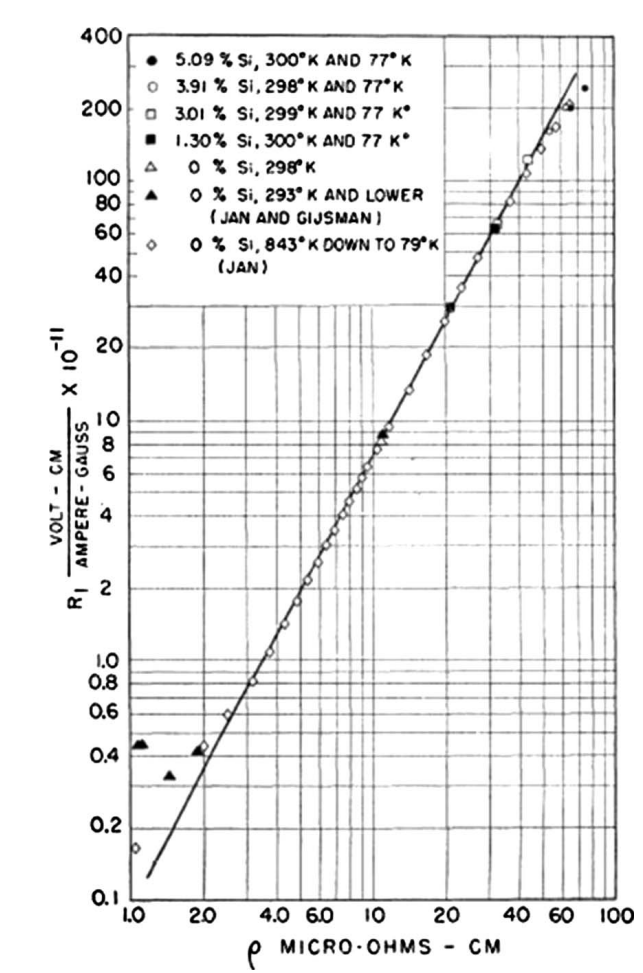
Early experimental data2 suggest
How do we measure the AHE conductivity? People have noted that the Hall effect in ferromagnetic and nonmagnetic metals are very different. In nonmagnetic metals, the Hall current comes the Lorentz force. In a ferromagnet,
References and notes