Lecture 11

03/27/2023, M.

Today

• Electric conductivity

• Boltzmann transport theory

Reading

• Girvin & Yang ch. 8

• Girvin & Yang ch. 10.2-10.3

1. Boltzmann transport

In the relaxation time approximation (弛豫时间近似)

Isotropic case, the longitudinal conductivity

This is recovers the Drude's law, with a little subtlety. In the Drude's law, the relaxation time should be ${\tau }_0$$\tau_0$ of the kinetic theory. Here, $\tau$$\tau$ is the transport relaxation time, from the Born approximation.

The anomalous Hall effect

Let's verify Eq. $\text{(2)}$$\eqref{eq:drude1}$ for the longitudinal conductivity explicitly, for an isotropic system at low temperatures

We obtain the conductivity

which differs from the Drude formula: $\tau ({\epsilon }_{\text{F}})$$\tau(\varepsilon_\text F)$ is the transport relaxation time at the Fermi energy, and $m^{\ast }$$m^*$ is the effective mass.

Alternatively,

where the mean free path (平均自由程) is defined as

The point is that conduction is a Fermi surface property!

we note that the diffusion constant is

and find

This last equation is called the Einstein relation. Thus, if a material is to conduct, we need both $D>0$$D>0$ and nonzero density of states.

A subtle point: there is heating

how can we pretend we can achieve steady state? The energy gets dissipated in the sample or in external circuit, via inelastic scattering, e.g. electron-phonon scattering. But we usually do not need to specify the details inelastic scattering in our linear-response calculation is that its effect (which gives rise to dissipation) is of order $|E{|}^2$$|E|^2$.

Back to Boltzmann equation

where $\delta k=-\tau qE/\hslash$$\delta k=-\tau q E/\hbar$.

Let $q=-e$$q=-e$, then $\delta k>0$$\delta k>0$ if $E>0$$E>0$

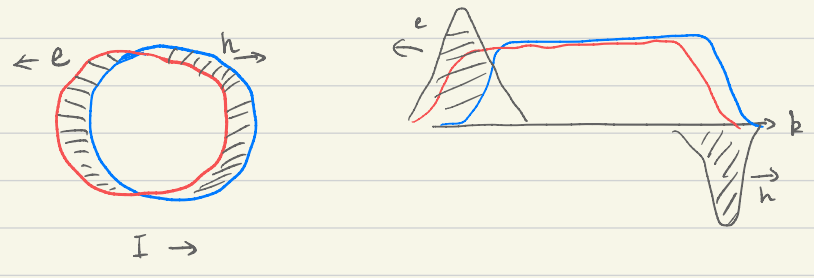
2. Einstein relation

The Einstein relation is quite general, independent of the Boltzmann equation. We now show it is required if an electron system is to achieve equilibrium.

$\tilde{\mu }$$\tilde \mu$ is the global or electrochemical potential, which is a constant in an equilibrium state. The local chemical potential $\mu$$\mu$ (which depends on the local electric potential ) determines the local electron density

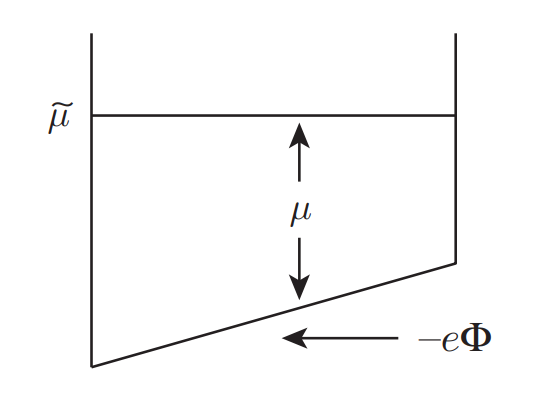
There is an electric current due to the electrochemical potential $\mathrm{\Phi }$$\Phi$

and a current due to diffusion

To achieve equilibrium, the should be no measurable flux anywhere. So at every point

we find from $-e\mathrm{\Phi }+\mu =\tilde{\mu }$$-e\Phi+\mu=\tilde \mu$ that

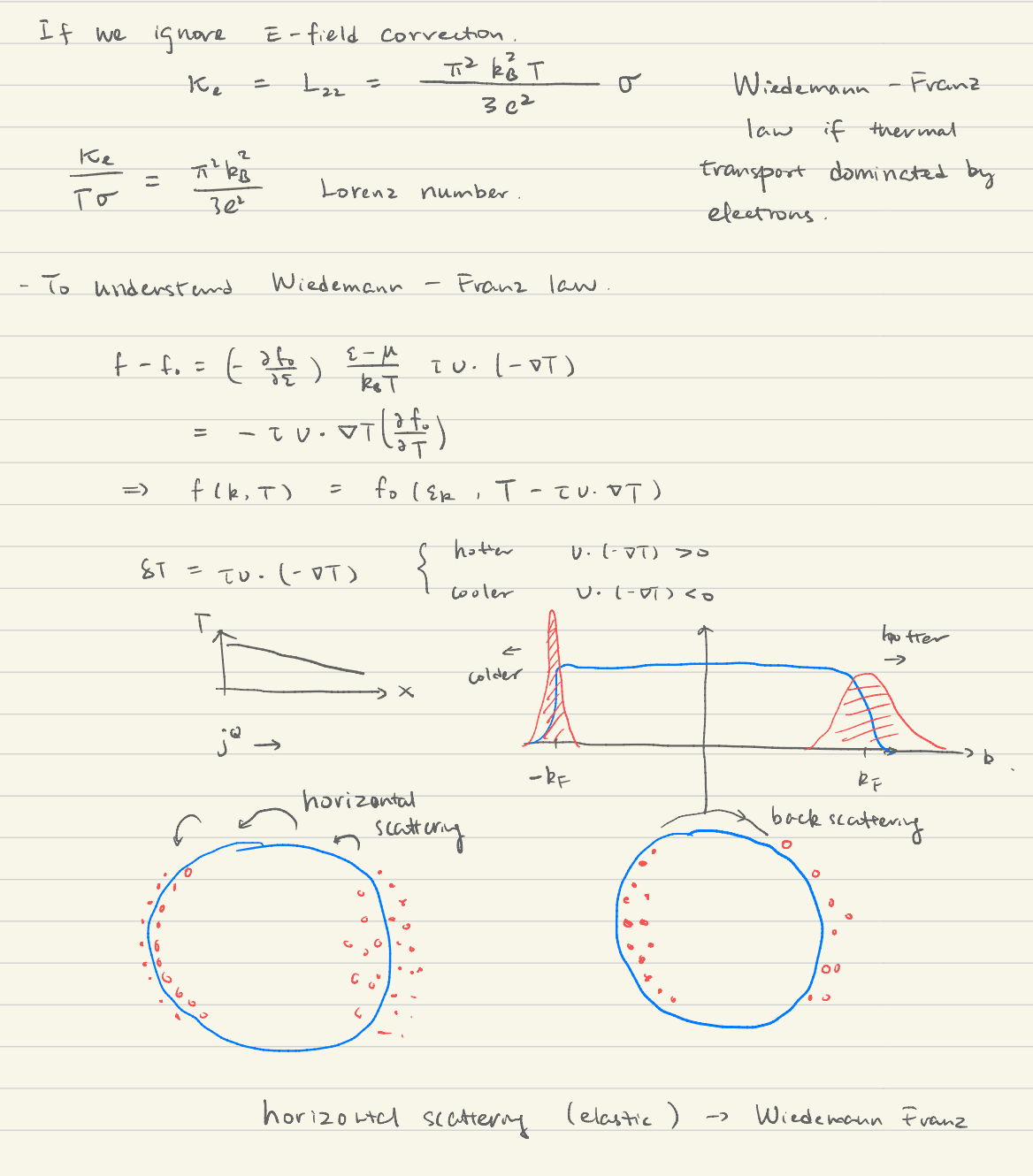
3. Thermal transport

4. Beyond Boltzmann theory

Quantum effects

• Shubnikov-de Haas oscillation: $\delta \sigma$$\delta \sigma$ oscillation in strong magnetic field, due to the change in the Landau spectrum with increasing B.

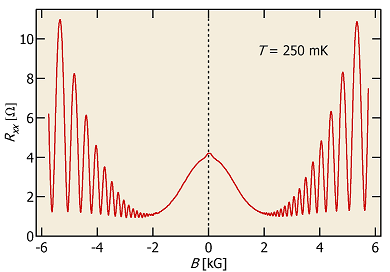
• De Haas–Van Alphen effect: the magnetic susceptibility of a pure metal crystal oscillates as the intensity of the magnetic field B is increased

• Localization: weak, strong, many-body.