Lecture 14

04/05/2023, Th.

Today

• Weak localization

• Strong localization

1. Weak localization

The quantum correction to conductivity is (roughly) proportional to the probability for the electron to traverse a closed (self-intersecting) loop without losing its coherence.

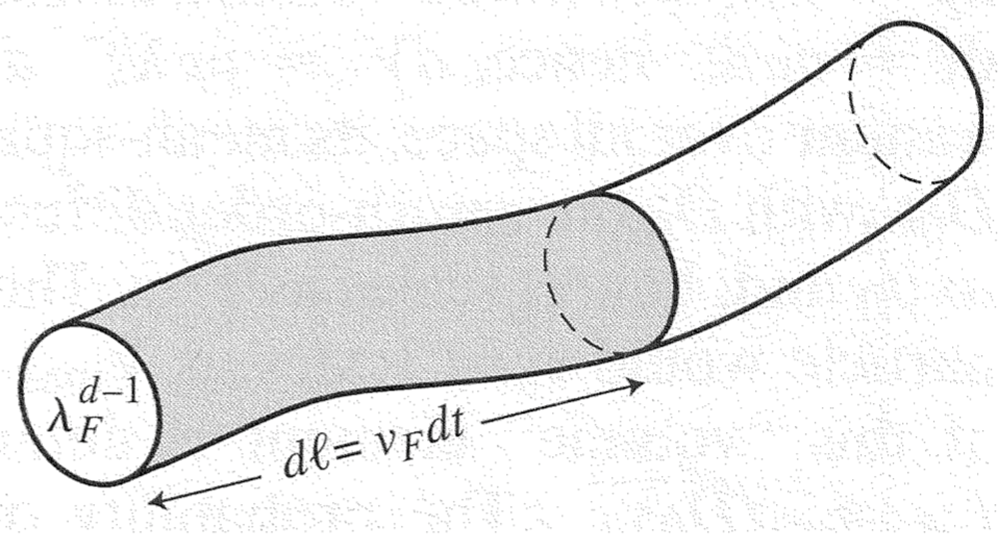
This probability would be zero for a classical particle, but for a quantum particle like an electron, we treat it as a tube of finite thickness of the order of its wavelength, $\lambda \sim 1/k_{\text{F}}$$\lambda\sim 1/k_\text F$. During time $t\gg \tau$$t\gg \tau$, the electron can visit any point by diffusion in a volume of the order $\sim {\ell }_D^d$$\sim\ell _D^d$. In order for self-intersection to occur during time interval $\text{d}t$$\text dt$, the electron has to enter a volume element

The correction is then proportional to the volume ratio

The minus sign comes from the expectation of localization in this case.

The lower bound of the integral is $\tau$$\tau$, because as we have argued, below this time scale, the transport is ballistic, but our arguments are only good for the diffusive regime. And the upper bound of the integral is ${\tau }_{\varphi }$$\tau_\phi$, the time scale below which the electron can be thought to keep coherence. Electrons can lose coherence through inelastic electron-electron and electron-phonon scattering, which leads to phase relaxation and breakdown of amplitude coherence.

Massage the Drude conductivity a little bit

where we have dropped order 1 factors. Multiplying ${\sigma }_0$$\sigma_0$ to the right-hand side of $\text{(2)}$$\eqref{eq:lec14-dsigma1}$, we find

Integrating, we find

First consider the $d=3$$d=3$ case. The correction is small, but can be interesting if we consider the dependence of ${\tau }_{\varphi }$$\tau_\phi$ on temperature. Dephasing occurs mostly through inelastic scattering of electrons by electrons and by phonons. In the former case (so we ignore phonon scattering, OK at low T),

Plug this into $\text{(5)}$$\eqref{eq:lec14-dsigma123}$, we find the temperature correction due to interference is of the order

Recall the scattering time due to electron-electron scattering depends on temperature via

So the Drude conductivity changes with temperature as

For phonon dominated scattering

Now we consider $d=2$$d=2$. The quantum correction for d = 2 diverges logarithmically as $\delta \sigma \sim -\log \left({\ell }_{\varphi }/\ell \right)$$\delta\sigma\sim-\log (\ell_\phi/\ell)$. Then for sufficiently large ${\ell }_{\varphi }$$\ell_\phi$ the system is fully localized.

But for intermediate ${\ell }_{\varphi }$$\ell_\phi$, the system may remain in the diffusive metallic regime, in which weak localization (WL) can be observed.

High-quality metallic film is very good for this kind of measurements.

• But how? Break the interference: Magnetic field, magnetic impurity, SOC, Berry phase.

There is magnetic phase as the electron closes up a loop. The Aharohnov-Bohm phase is proportional to the magnetic flux $\mathrm{\Phi }$$\Phi$ enclosed by a loop in real space

where the flux quantum is taken to be

So the phase difference is between $P$$P$ and $\tilde{P}$$\tilde P$ is

So the perfect interference of self-intersecting paths get disrupted by the magnetic phase, which will supress the localization effects, and in turn leads to a negative magnetoresistance (磁阻).

Let's try and estimate the magnitude of the negative MR. If we use the diffusion length ${\ell }_D(t)=\sqrt{2dDt}$$\ell_D(t)=\sqrt{2dDt}$ to estimate the size of the loop, then the flux is

Define ${\tau }_B$$\tau_B$ to be the time for $\mathrm{\Phi }/{\mathrm{\Phi }}_0$$\Phi/\Phi_0$ to reach 1/2, such that $\mathrm{\Delta }\phi =2\pi$$\Delta\varphi=2\pi$

where the magnetic length is defined as

Obviously, ${\tau }_B$$\tau_B$ is the time scale beyond which decoherence is irrelevant. Or ${\tau }_B$$\tau_B$ can replace ${\tau }_{\varphi }$$\tau_\phi$ if ${\tau }_B\ll {\tau }_{\varphi }$$\tau_B\ll \tau_\phi$, and we have for $d=2$$d=2$

For small $B$$B$-field, there is near-singular $\log B$$\log B$ feature in the magnetoconductivity.

The full theory of weak localization was developed in the Hikami-Larkin-Nagaoka equation (Prog. Theo. Phys. 63, 70 (1980)).

If ${\tau }_B\ll {\tau }_{\varphi }$$\tau_B\ll \tau_\phi$, the first term dominates because $\underset{x\to 0}{lim}\frac{\log x}{\psi (x+1/2)}=\mathrm{\infty }$$\lim _{x \rightarrow 0} \frac{\log x}{\psi(x+1 / 2)}=\infty$, so we recover the above result in $\text{(18)}$$\eqref{eq:lec14-magcon}$.

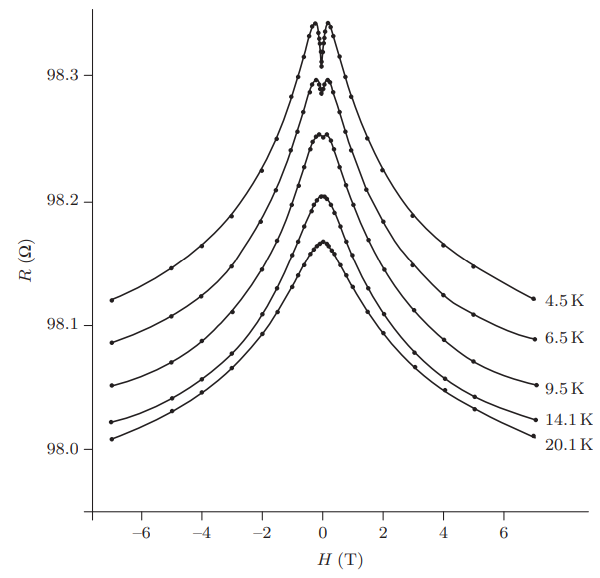
The above figure (Figure 11.6 from G&Y) shows experimental transport data illustrating the negative magnetoresistance of a 2D disordered system caused by the destruction of time-reversal symmetry as a magnetic field is applied. At weak fields and the lowest temperatures one sees a small region of positive magnetoresistance.

This corresponds to a negative change in conductivity in magnetic field. This means without magnetic field destroying the interference, the electrons are more delocalized.

This turns out to be the result of spin-orbit scattering, by heavy atoms (as impurities). The phenomena is called weak anti-localization.

Flux-threaded lithium tube:

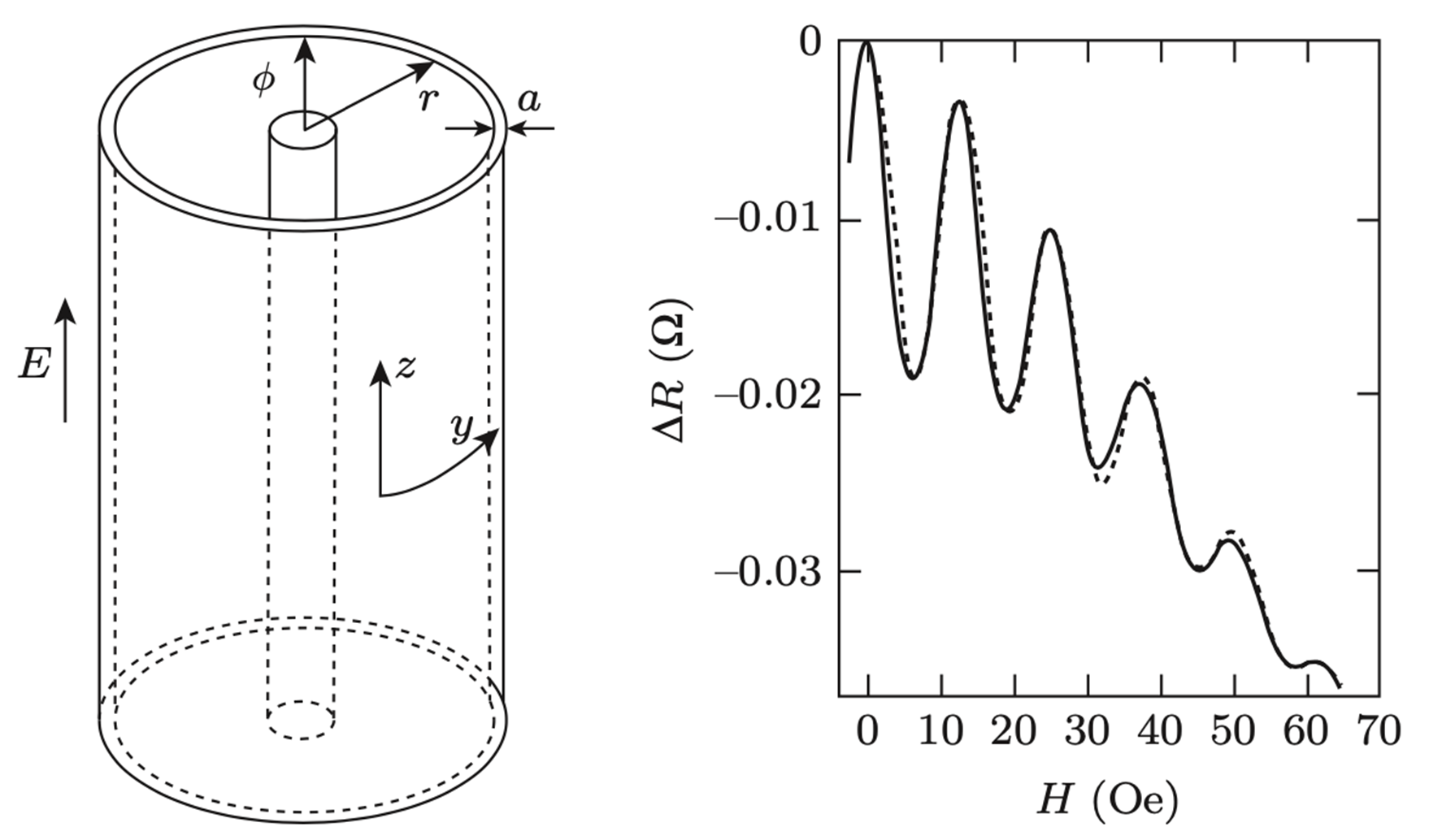
as an electron move across the tubular conductor, it can follow self-intersecting paths with different winding numbers

Then the A-B phase difference is

We thus expect the magnetoresistance to oscillate with , with period 0/2. This is indeed seen experimentally.

2. Thouless scaling idea

We have seen in the Landauer model that the resistances do not add. This is a consequence of the nonlocality of quantum transport. This means there can be nontrivial dependence on the system size. So how does conductance $G$$G$ depend on $L$$L$? Some early ideas were due to David Thouless.

For a metal block of size $L^d$$L^d$

where

is the time scale for an electron to diffuse across the block, and

is the energy level spacing (能级间隔).

Introduce a Thouless energy

which is the energy uncertainty associated with diffusion.

here $g(L)$$g(L)$ is a dimensionless conductance, depending on the system size.

In Thouless's picture, conductance is determined by the level spacing $\mathrm{\Delta }E$$\Delta E$ and the Thouless energy, $E_{\text{T}}$$E_\text T$. The Thouless energy reflects the change of level energy from one surface to another, so it reflects the sensitivity to boundary conditions.

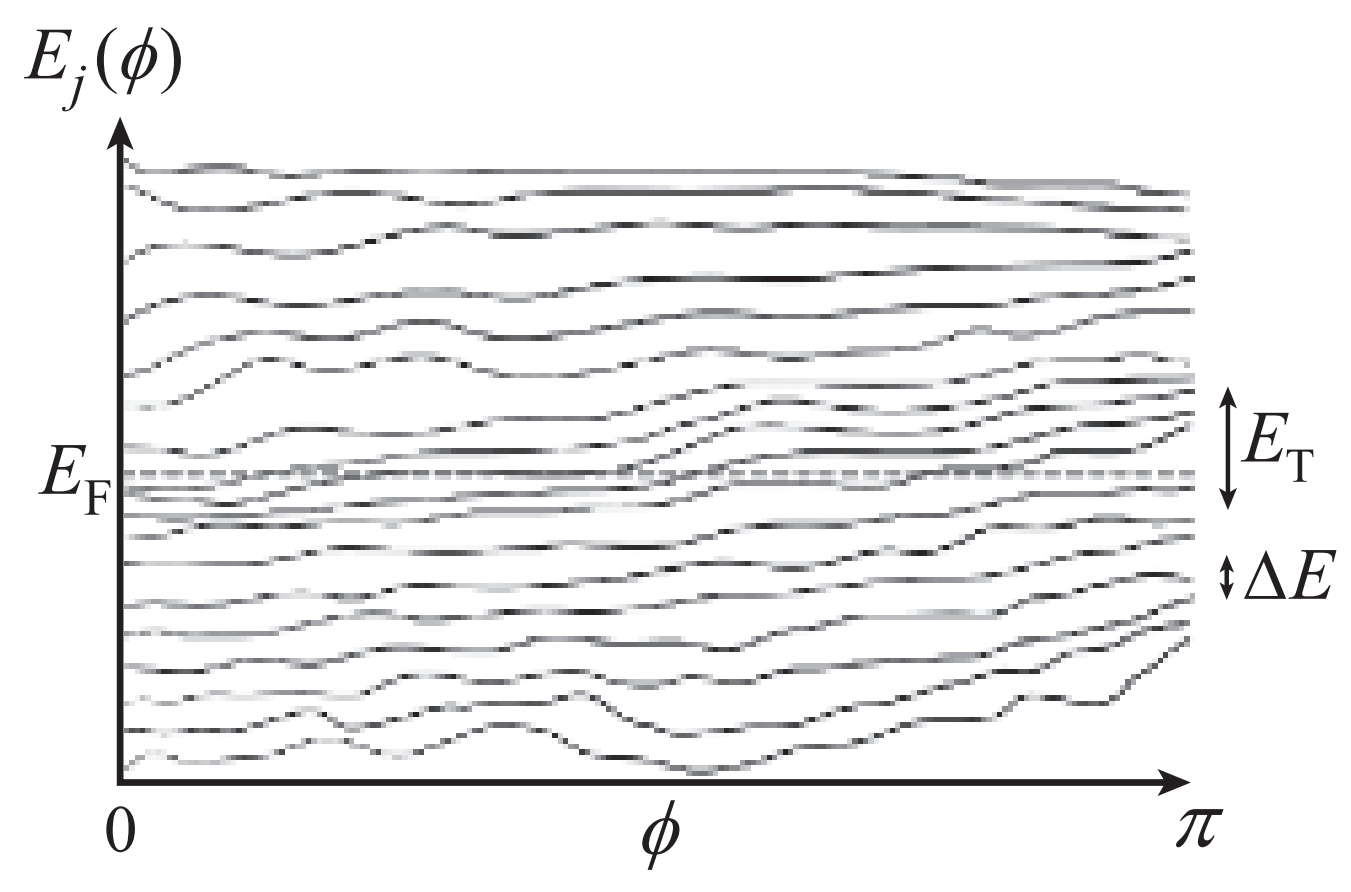
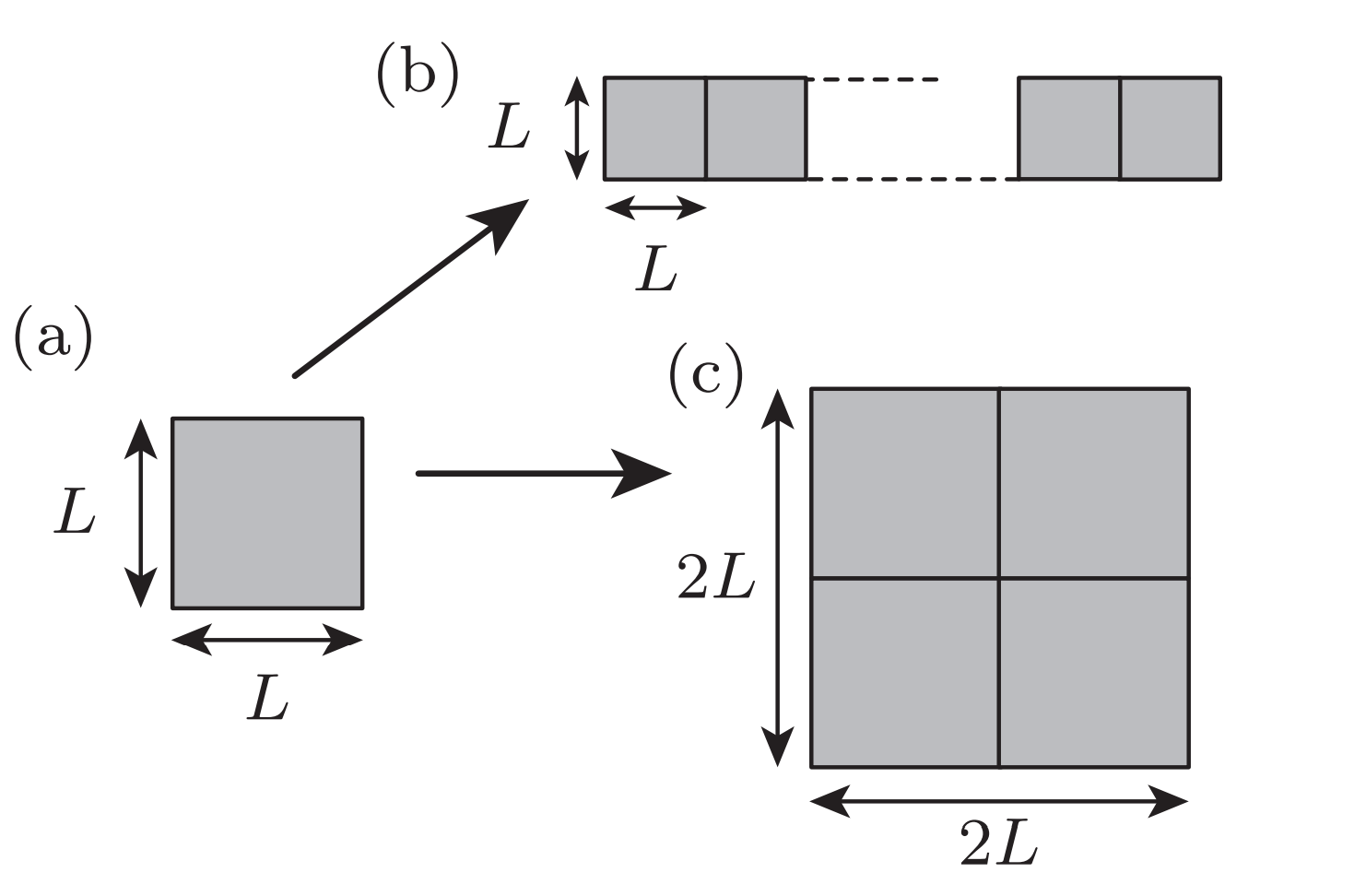
Let us build a metal form bottom up,

For large perturbation $H_T$$H_T$, $E_T>\mathrm{\Delta }E$$E_T>\Delta E$, perturbation theory will not work. But Thouless suggest that we may have a scaling function

Here, the scaling function $F(g)$$F(g)$ is independent of size or other details of the system. This is the scaling hypothesis of Thouless.

3. Anderson localization

In 1979, the gang-of-four paper by Abrahams et al argues that the scaling function not only exist, but also is universal, independent of microscopic details, such as band structure, impurity, etc.

The scaling function $\beta$$\beta$ is a function of $g$$g$ only, independent of $L$$L$ or other details, and should be universal (well, given the dimensionality and symmetry, the discussion of the latter we will not get into). The exact form of $\beta$$\beta$ is not known, and probably unimportant. It is necessary to figure our the behaviour of $\beta$$\beta$ in certain limits.

• in good conductors, the Ohm's law holds. So $G(L)=\sigma L^{d-2}$$G(L)=\sigma L^{d-2}$, so

  $$\begin{array}{}\text{(30)}& \beta (g)=d-2\end{array}$$

• The opposite limit is the localized regime (like the Anderson insulator)

  $$\begin{array}{}\text{(31)}& g(L)\sim e^{-L/\xi }.\end{array}$$

  so

  $$\begin{array}{}\text{(32)}& \beta (g)=-L/\xi =\log g\end{array}$$

• Abrams et al further assumed that $\beta (g)$$\beta(g)$ is a smooth and monotonic (单调) function of $g$$g$. The latter is not always true. So we make a smooth interpolation between the good metal limit and insulating limit. In the large $g$$g$ limit, it is expanded as

  $$\begin{array}{}\text{(33)}& \beta (g)=d-2-a/g+O\left(1/g^2\right)\end{array}$$

  here $a$$a$ is a parameter whose sign depends on the universality class (普适类), based on symmetry classification (time-reversal and spin rotation, etc).

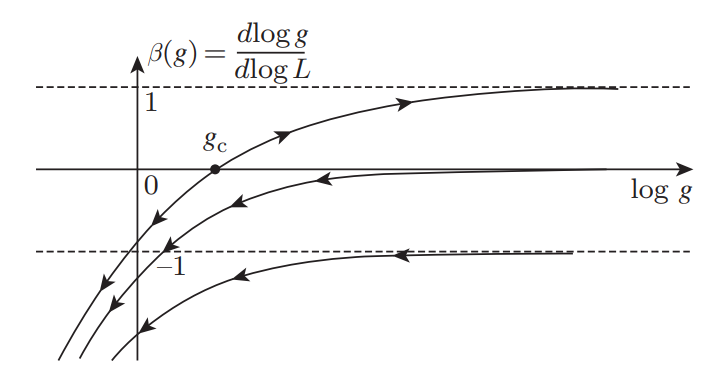
• d=3:

  • large g: a good metal stays a good metal

  • small g, $\beta <0$$\beta<0$: a poor metal gets localized -- Anderson insulator

  • $\beta (g_c)=0$$\beta(g_c)=0$: unstable fixed point, and critical point.

• d=1, 2: always localized for small $g$$g$

• d=1: always flow to insulating state: strong localization

• d=2: in the large g regime, g decreases slowly. It is possible to observe weak localization.

Some recent developments:

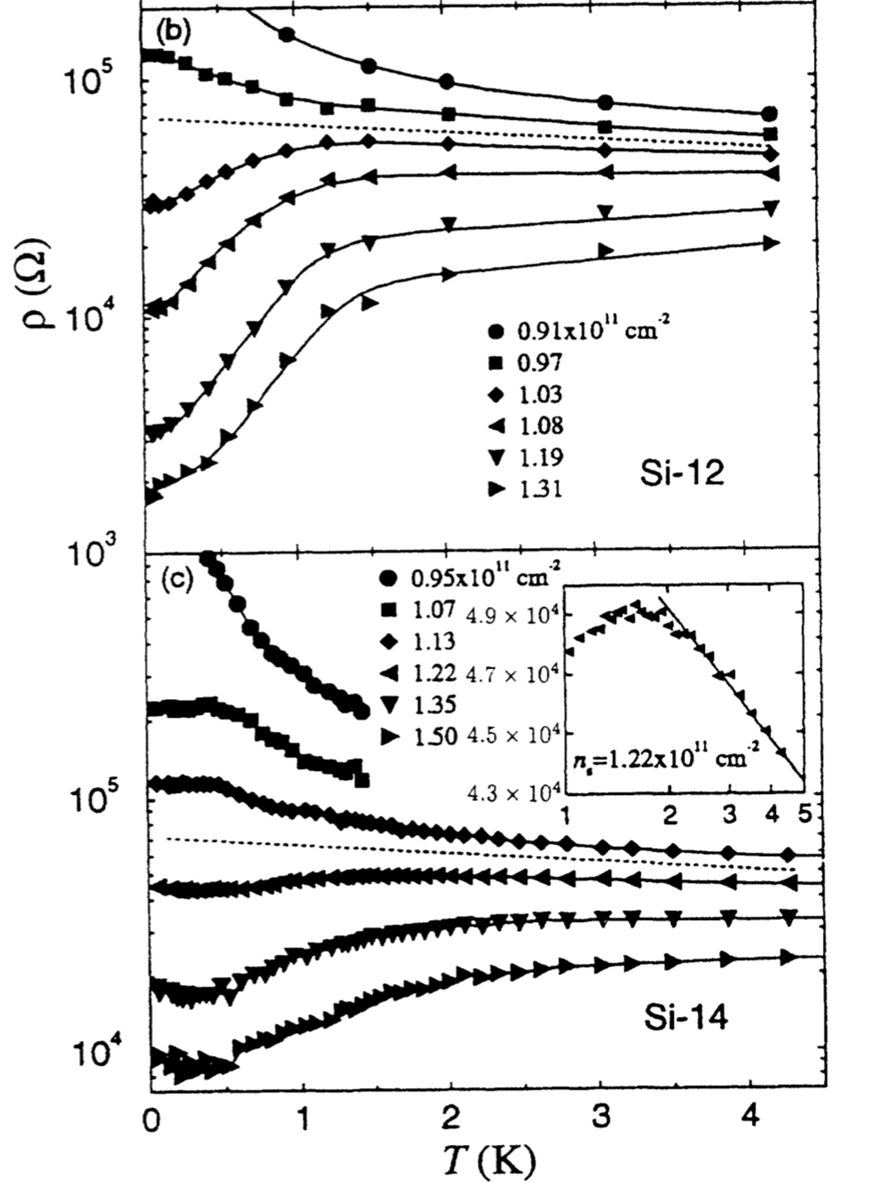
• In high-quality 2D films, there is a critical electron concentration, beyond which the system does not localize.

• That is, as $T\to 0$$T→0$, there is a concentration-driven MIT, which breaks the universality of the scaling law for d = 2.

• The scaling function need not be monotonic. For d = 2, and $g\gg g_c$$g≫g_c$

  $$\begin{array}{}\text{(34)}& \beta (g)=d-2+\frac{a}{g^{\alpha }}+O\left(g^{-2}\right)\end{array}$$