Lecture 15

04/10/23, M.

Next: Berry phase and topology of Bloch bands

Ch. 13, 12, 14 of G&Y.

1. Geometry and topology

Instead of offering a systematic survey of concepts of topology, I offer an appetizer by with the Gauss-Bonnett theorem

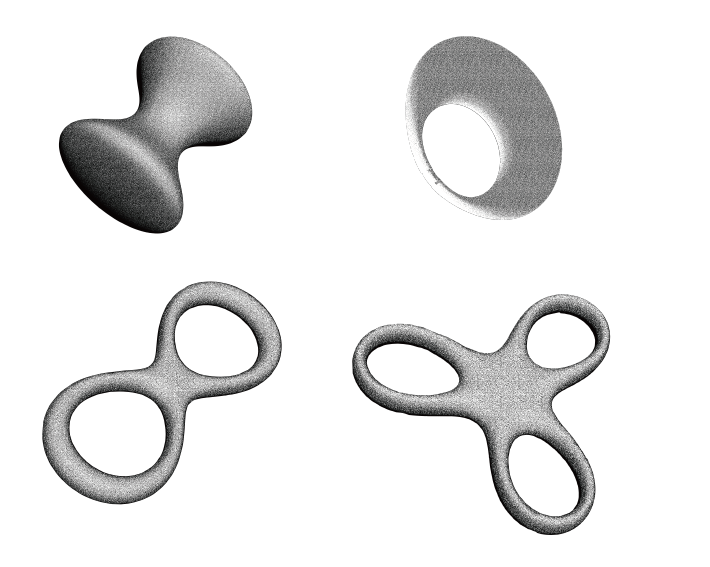
The Gauss–Bonnet theorem provides a quantitative relation between the curvature (a local quantity) and its topology (a global property) of a surface.

\begin{matrix} (1) & \int_{M} K d A + \int_{\partial M} k_{g} d s = 2 π χ (M) \end{matrix}

$\chi$ $M$ , which is related the genus (number of holes) as

\begin{matrix} (2) & χ = 2 - 2 g - b, \end{matrix}

$b$ is the surface term and vanishes for a closed surface.

$r$ , it Gaussian curvature is

\begin{matrix} (3) & K = \frac{1}{r^{2}} \end{matrix}

Then

\begin{matrix} (4) & 2 π χ = \int_{S^{2}} d A \frac{1}{r^{2}} = \frac{A}{r^{2}} = 4 π = 2 π \times 2 \end{matrix}

$\chi=2$ for sphere.

continuously $\chi$ stays the same as long as two surfaces can transform into each other.

$R^3$ $S$ $\boldsymbol r=\boldsymbol r(u,v)$ $p$ on the surface a unit normal is given by

\begin{matrix} (5) & n (p) = \pm \frac{r_{u} \times r_{v}}{| r_{u} \times r_{v} |} (p) \end{matrix}

This is called the Gauss map, which maps a surface on to a unit sphere. The Gaussian curvature is

\begin{matrix} (6) & κ = \frac{| n_{u} \times n_{v} |}{| r_{u} \times r_{v} |} \end{matrix}

\begin{matrix} (7) & \begin{matrix} \int_{M} κ d A = \int_{M} \frac{| n_{u} \times n_{v} |}{| r_{u} \times r_{v} |} | r_{u} \times r_{v} | d u d v \\ = \int_{S^{2}} | n_{u} \times n_{v} | d u d v \\ = area of n on S^{2} \end{matrix} \end{matrix}

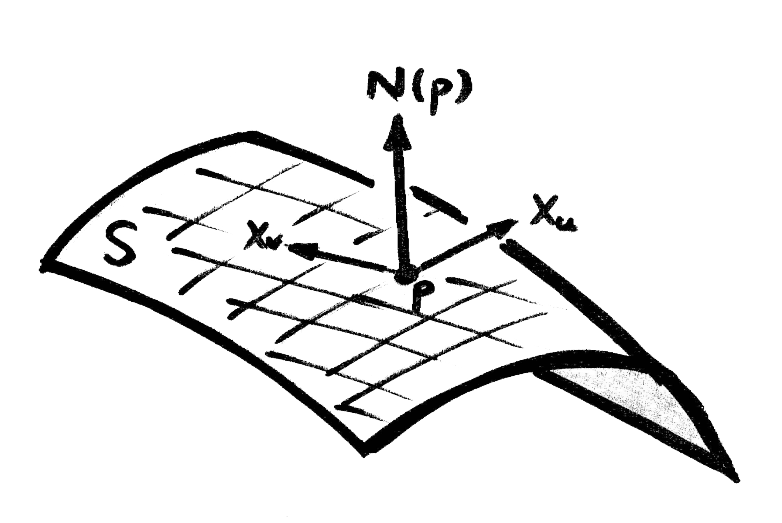
So Gaussian curvature is like the Jacobian of the Gauss map.

$T^2= S^1\times S^1$ .

\begin{matrix} (8) & \begin{aligned} x (u, v) = (R + r \cos v) \cos u \\ y (u, v) = (R + r \cos v) \sin u \\ z (u, v) = r \sin v \end{aligned} \end{matrix}

$u,v\in[0,2\pi], R>r$ .

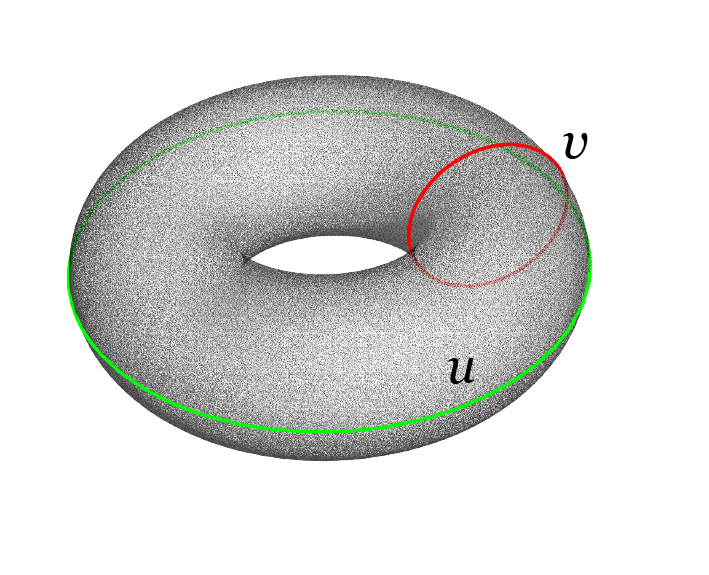
$\boldsymbol r(u,v)$ on the torus, the normal is

\begin{matrix} (9) & n = (\cos u \cos v, \sin u \cos v, \sin v) \end{matrix}

We find the Gaussian curvature to be

\begin{matrix} (10) & κ = \frac{\cos v}{r (R + r \cos v)} \end{matrix}

The surface element is

\begin{matrix} (11) & d A = r_{u} \times r_{v} d u d v = r (R + r \cos v) d u d v \end{matrix}

$\chi=0$ $g=1$ , i.e., one hole.

Quantization $\chi$ is quantized.

Global $\chi$ is a global quantity, by virtue of the integral.

Invariant $\chi$ is quantized and invariant under continuous deformation, it is called a topological invariant (拓扑不变量).

New physics:

quantized property, robust against perturbation, and interaction
phase change: no symmetry change

Our goal: topology of Bloch bands

2. Geometric phase

We consider the adiabatic evolution of a semiclassical system.

The instantaneous eigen states

\begin{matrix} (12) & H (λ (t)) | n (λ (t)) ⟩ = E_{n} (λ (t)) | n (λ (t)) ⟩ \end{matrix}

$t=0$

\begin{matrix} (13) & ψ (0) = n (λ (0)) \end{matrix}

Adiabatic limit (绝热极限):

\begin{matrix} (14) & ψ (t) = e^{- \frac{i}{ℏ} \int_{0}^{t} E_{n} (λ (t^{'})) d t^{'}} e^{i γ_{n} (t)} | n (λ (t)) ⟩ \end{matrix}

The Schrodinger equation

\begin{matrix} (15) & i ℏ \partial_{t} | ψ (t) ⟩ = H (λ (t)) | ψ (t) ⟩ \end{matrix}

Inserting the adiabatic wavefunction into it, we find

\begin{matrix} (16) & [E_{n} (λ (t)) - ℏ {\dot{γ}}_{n} + i ℏ \partial_{t}] | n (λ (t)) ⟩ = E_{n} (λ (t)) | n (λ (t)) ⟩ \end{matrix}

where

\begin{matrix} (17) & {\dot{γ}}_{n} = \underset{Berry connection A (λ)}{\underset{⏟}{⟨ n (λ) | i \partial_{λ} | n (λ) ⟩}} \cdot \dot{λ} \end{matrix}

Integrating, we find the geometric phase (几何相位)

\begin{matrix} (18) & γ_{n} = \int_{0}^{t} {\dot{γ}}_{n} d t = \int_{λ (0)}^{λ (t)} A \cdot d λ \end{matrix}

$\gamma_n$ is called geometric because it depends on the path.

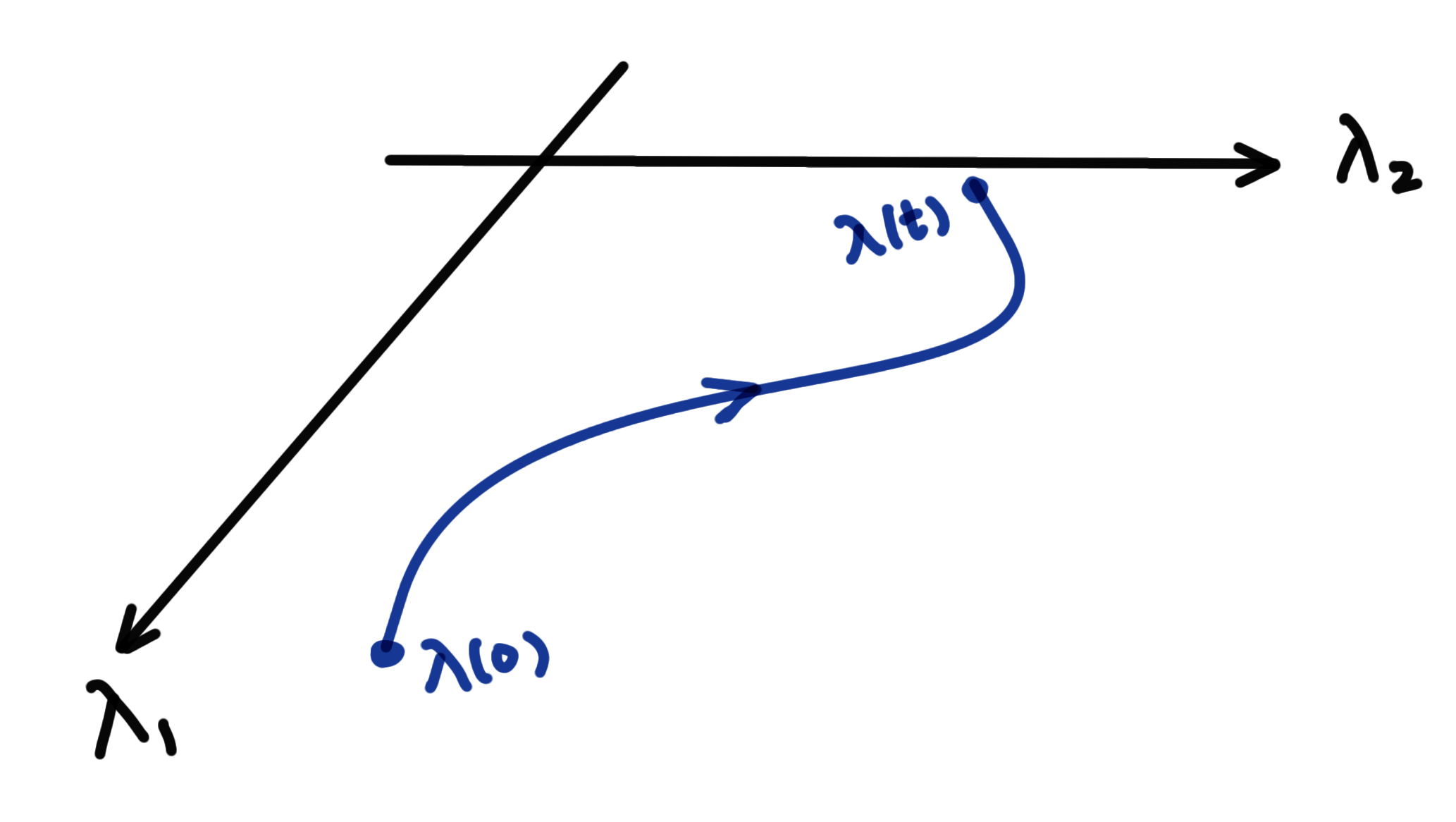
U(1) gauge transformation

\begin{matrix} (19) & | n (λ) ⟩ \to e^{i χ (λ)} | n (λ) ⟩ \end{matrix}

\begin{matrix} (20) & \begin{aligned} A_{α} & \to A_{α} - \frac{\partial χ}{\partial λ^{α}} \\ γ_{n} & \to γ_{n} - χ (λ (t)) + χ (λ (0)) \end{aligned} \end{matrix}

$\gamma_n$ can be gauged away, so it can have any measurable effect. This is because in quantum mechanics, for a quantity to be measurable, it must be gauge invariant.

3. Berry phase

Now we inspect the geometric phase over a loop

\begin{matrix} (21) & \begin{matrix} γ = \oint_{\partial Σ} A \cdot d λ \\ = \frac{1}{2} \int_{Σ} Ω_{a b} d λ_{a} \land d λ_{b} \end{matrix} \end{matrix}

$\Omega_{ab}$ is an antisymmetric rank-2 tensor, the Berry curvature (or Berry flux)

\begin{matrix} (22) & Ω_{a b} = \frac{\partial A_{b}}{\partial λ_{a}} - \frac{\partial A_{a}}{\partial λ_{b}} \end{matrix}

Example: 2D Dirac fermion in graphene. Take one of the valleys

\begin{matrix} (23) & \begin{matrix} H (k) = v (\begin{array}{cc} 0 & k_{x} - i k_{y} \\ k_{x} + i k_{y} & 0 \end{array}) \end{matrix} \end{matrix}

\begin{matrix} (24) & \begin{matrix} | ψ_{k} ⟩ = \frac{1}{\sqrt{2}} (\begin{array}{l} S \\ e^{i φ_{k}} \end{array}), \tan φ_{k} = k_{y} / k_{x} s = \pm 1 \end{matrix} \end{matrix}

with the dispersion relations

\begin{matrix} (25) & ε_{s k} = s ℏ v k \end{matrix}

For the Berry connection

\begin{matrix} (26) & \begin{matrix} A_{k} = \frac{1}{2} (s, e^{- i φ}) i \frac{\partial}{\partial k} (\begin{matrix} s \\ e^{+ i φ} \end{matrix}) \\ - \frac{1}{2} \partial_{k} φ \end{matrix} \end{matrix}

So the Berry phase for an electron to revolve around the Fermi surface

\begin{matrix} (27) & γ = - \frac{1}{2} \oint d k \partial_{k} φ = - π . \end{matrix}

$\pi$ Berry phase.

This has very important consequences for transport in graphene. Instead of displaying enhancement of backscattering, there is a suppression of backscattering.

But there is a problem. The Berry curvature

\begin{matrix} (28) & Ω_{k_{x} k_{y}} = \frac{\partial A_{y}}{\partial k_{x}} - \frac{\partial A_{x}}{\partial k_{y}} = 0 \end{matrix}

\begin{matrix} (29) & \int_{O} d^{2} k Ω_{k_{x} k_{y}} = 0 \end{matrix}

How is this compatible with the Stokes' theorem? The answer is: there is singularity.