Lecture 16
04/13/2023, Th.
Today
Berry connection and curvature
Examples: A-B phase, two-level system
Bloch bands
1. Multiband expansion for
We use the fact
If
Then
Finally we have
2. A-B phase a Berry phase
Aharonov-Bohm's phase us a quantum mechanical phenomenon, where a charged particle can pick up a phase in its wavefunction, although it is confined to a region where magnetic field is zero. This is so because even though in the region where the charged particle travels
This can be derived heuristically in a semiclassical approximation of the path integral, which says the transition is characterized by the phase of the classical path. The amplitude is
where
with
So there is a magnetic change of phase
Consider the electron goes from 1 to 2 via
which cannot be gauged away, since

We now illustrate how this phase can be formulated in terms of a Berry phase. We suppose the charged particle is an electron confined in a box (a confining potential), and is moved along with the box around the magnetic flux.
Without magnetic field,
Now turn on the
Because
The Berry connection
The Berry phase
Then we see that A-B phase is just the Berry phase.
3. Two-level system
The Hamiltonian of a two-level system can be written as
We can write the vector
Then there are two branches,
Let's compute the Berry connection
So the Berry curvature is
If we keep
So if
because
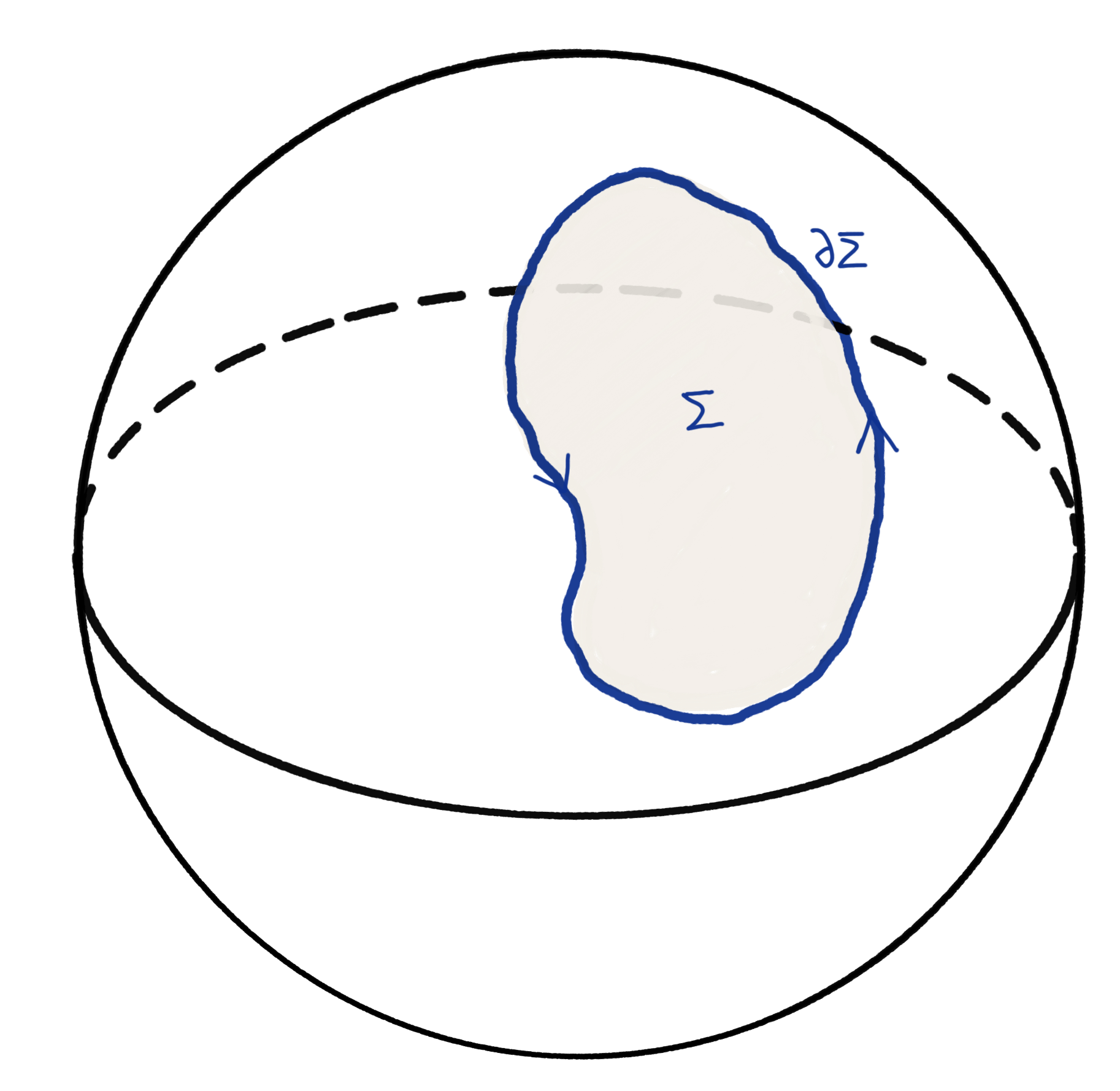
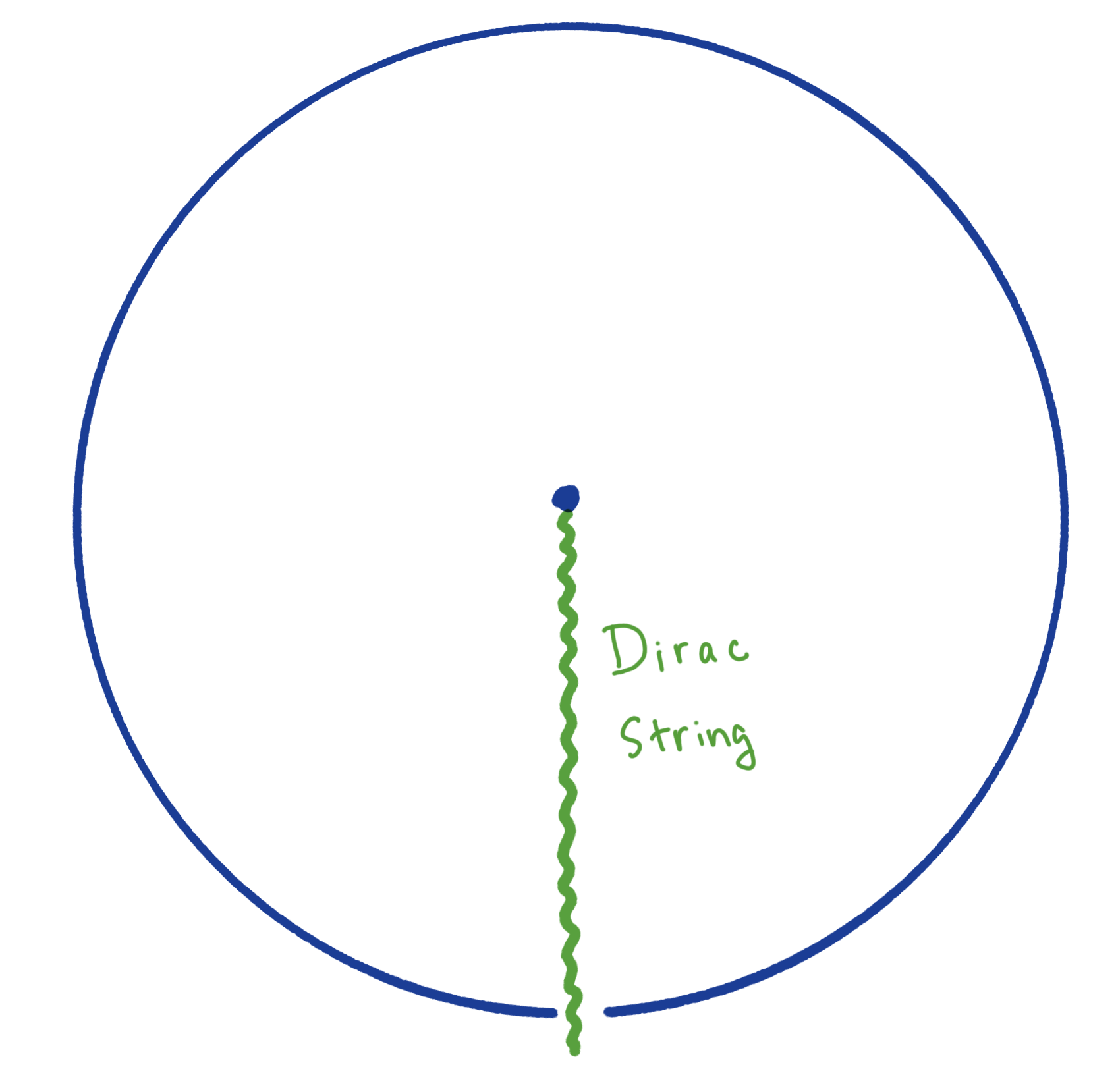
The contradiction arises from the the fact that
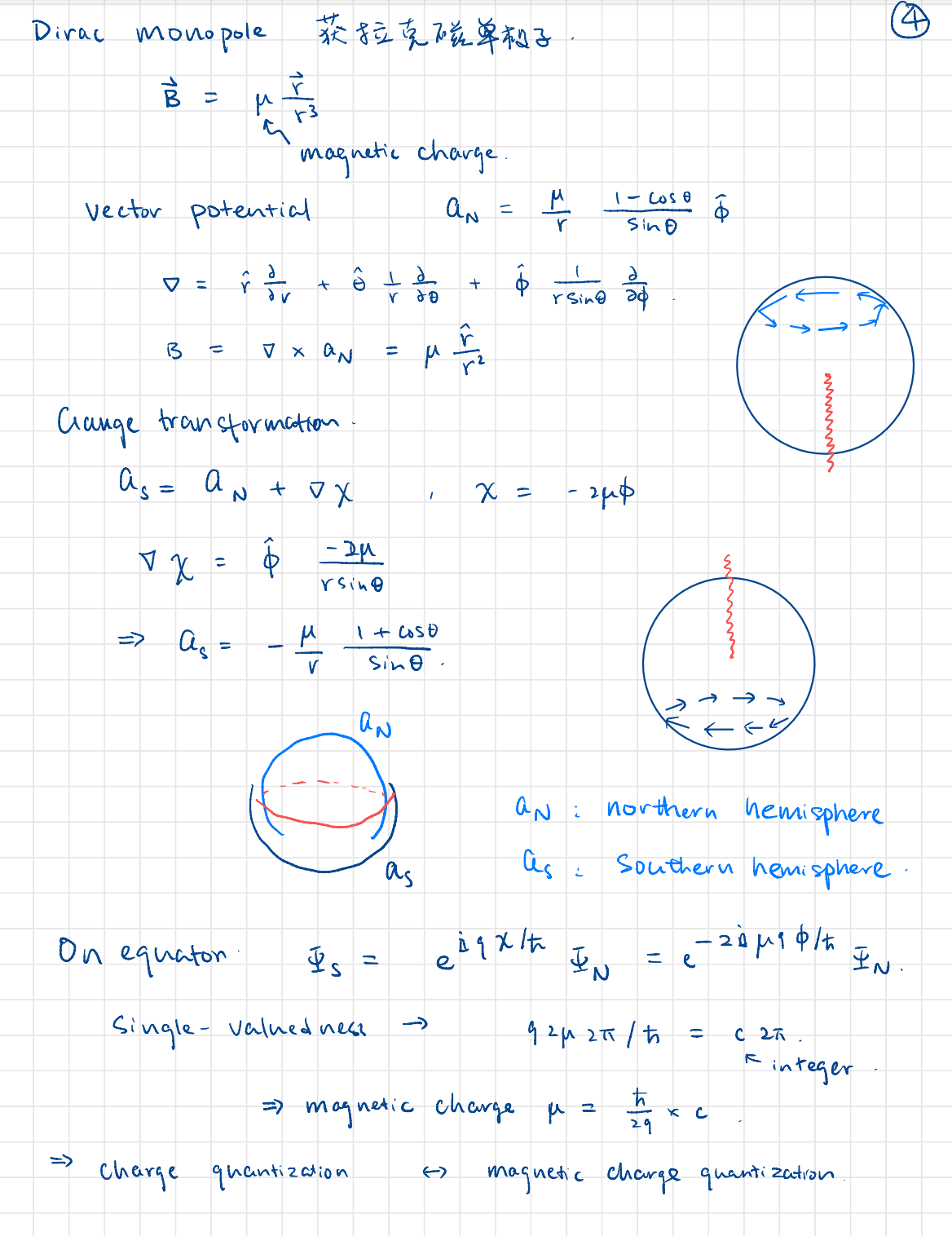
This is analogous to the Dirac's magnetic monopole, if we switch to the Cartesian coordinates
we find
which is singular at the origin.
4. Geometric properties of Bloch bands
For a single electron in a periodic potential, Bloch theorem says its eigenstates are irreducible representation of lattice translation
where the Bloch function has the following property
We call
We can now make the following transformation
which we will call the Bloch Hamiltonian. Then we have the following Schrodinger equation
We then define the Berry connection (again) of Bloch bands
Note that by our normalization convention,
For this course, we will focus on usually problems involving a single band. The one-band (Abelian) Berry connection is
with which we can introduce the Berry curvature (again, Abelian)
Let's now place the system in a uniform electric field
The crystal Hamiltonian is
And the Bloch Hamiltonian
but we may just define a new wavevector that depends on time
which admits the same eigenstates with time-dependent
So
Now consider the first-order wavefunction
The velocity operator
So the velocity to the first order of perturbation
where the first term is the group velocity of the nth Bloch band, and the second term is the anomalous velocity (we will see how it reduces to the anomalous velocity in the anomalous Hall effect shortly).
We note the following: for
we find that
So we have
where
So combining with the expression for
which is the same as what we have obtained from semiclassical dynamics.