Lecture 18
04/24/23, M.
Today
Winding number
Bulk-boundary correspondence
Anomalous Hall effect quantized
1. Winding number
The 1D Hamiltonian matrix
We require
Then we have map
where
The circles form a group by path composition, which is part of the elementary discussoin in algebraic topology, which we cannot go into any details here.
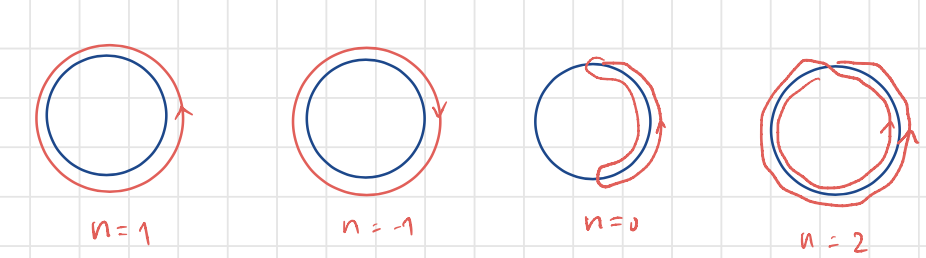
In integer
2. The boundary state
Join

The region between the two chains shows a slow (adiabatic) transition from
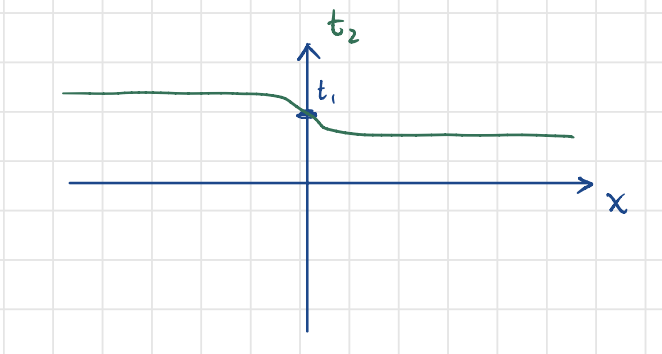
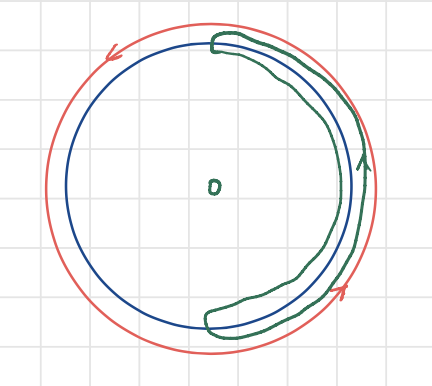
As the image of
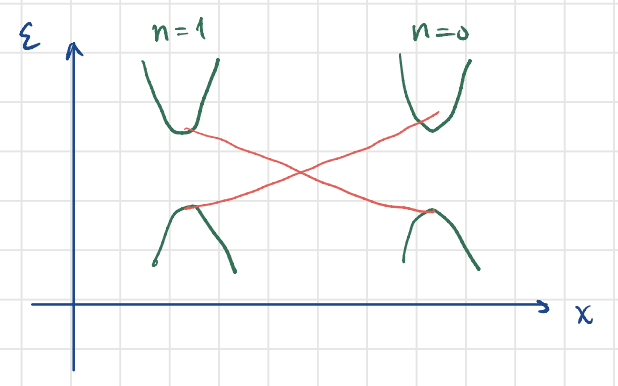
The winding number is a topological numer classifiying the two phases on the chain. And as the topology changes continuously from one region of the space to another, keeping the symmetry unchanged (chiral symmetry in this case), there is bound to be a place where the gap closes. This is called the principle of bulk-boundary correspondence.
The boundary states arising due to change of topology are then given the name: topologically protected boundary (edge, or surface) states, or zero modes sometimes.
Let us work out the boundary states explicitly. Near
Set
The Schrodinger equation then reads
So,
The zero mode then corresponds to
Consider two regimes:
which means
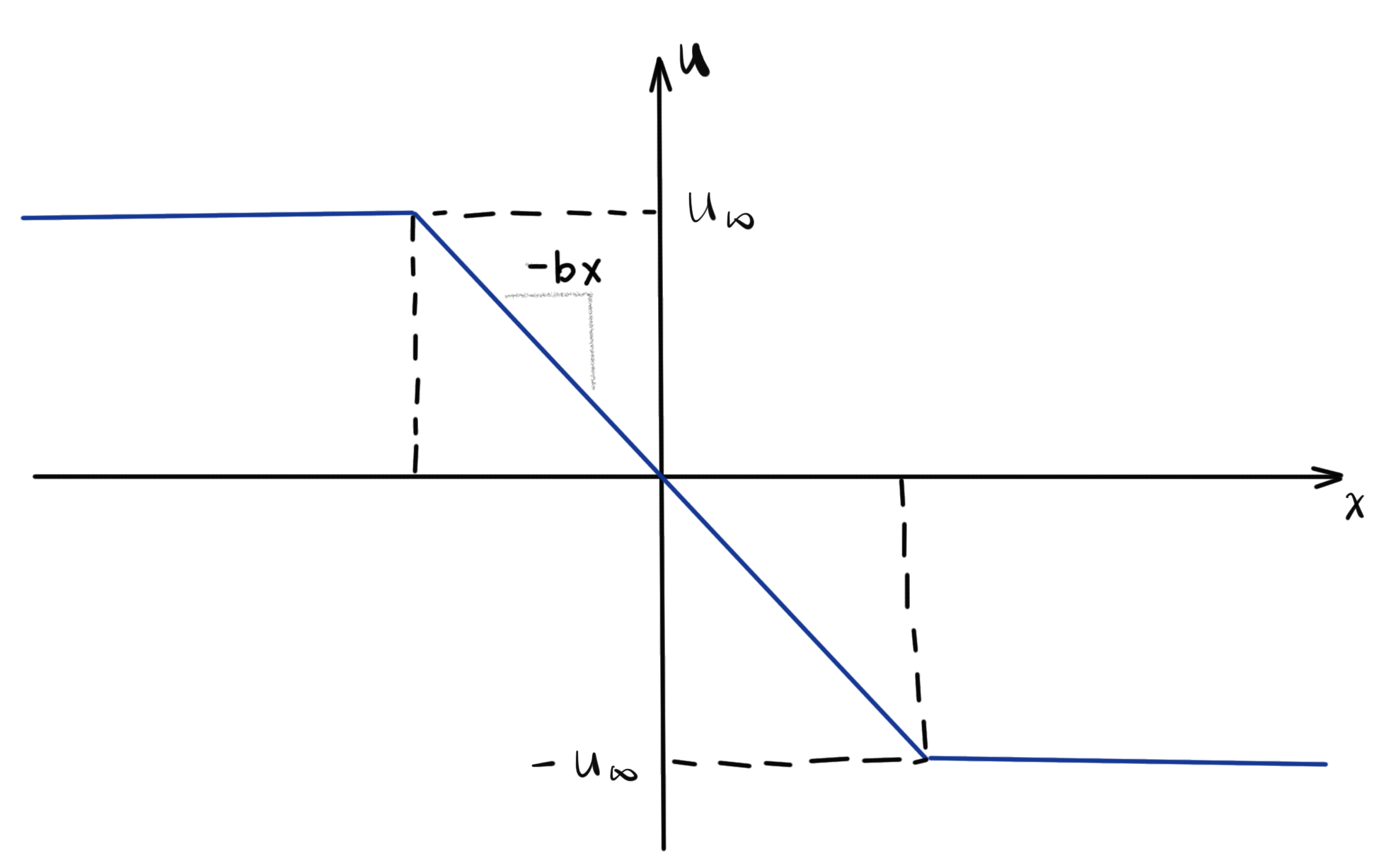
on the interval
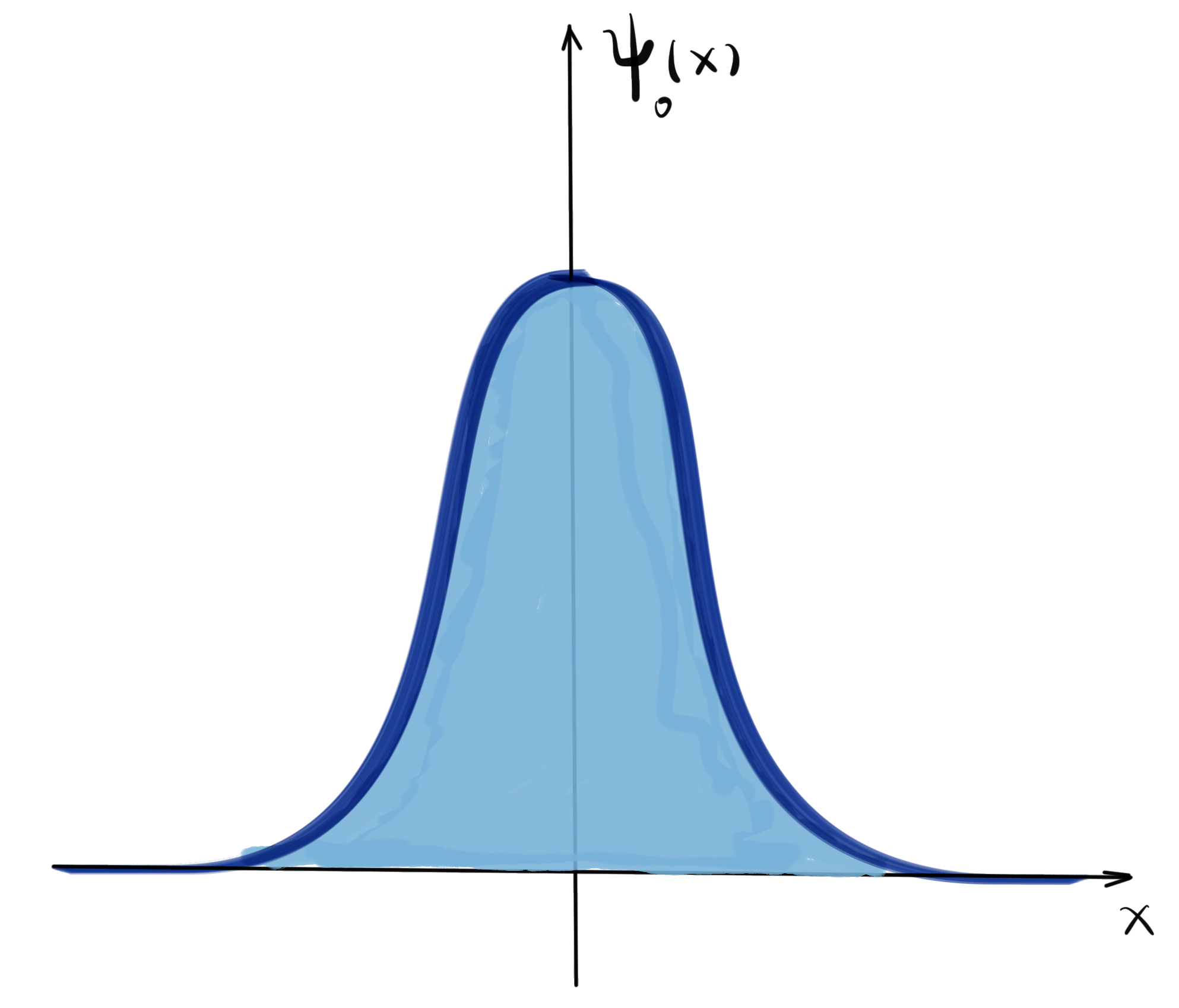
So we have confirmed that there are zero modes localized on the boundary, which is an initial demonstration of the bulk boundary correspondence.
3. 2D Dirac fermion with mass
The Hamiltonian
The Berry flux
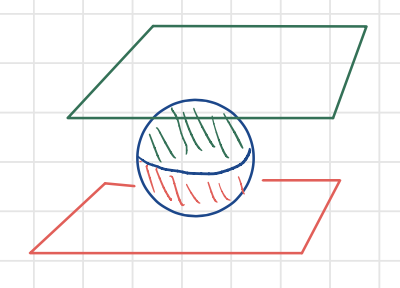
If we can design a graphene with a pair of massive Dirac Fermions with the same sign of masses, then the total Berry flux will take a integer, nonzero value of
Indeed, this corresponds to the so-called Haldane model, first proposed by Duncane Haldane in 1988.
Consider spinless elecrtron on a honeycomb lattice, with nearest-nerighbor (NN最近邻) and next-nearest-neighbor (NNN 次近邻) hoppings
It should be noticed that the NNN hopping cannot open a band gap, as the Dirac point is protected by inversion and time-reversal symmetries. The NNN hopping breaks neither.
To open a band gap, Haldane introduced a staggered (交错的) magnetic field
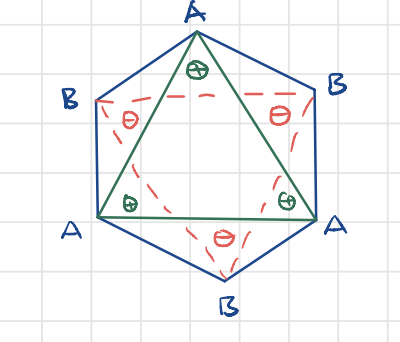
Consider the A sites. As the electron moves around a triangle, as shown below, it picks up an Aharonov-Bohm's phase. We can average the phase to the three bonds, because of the 3-fold rotational symmetry
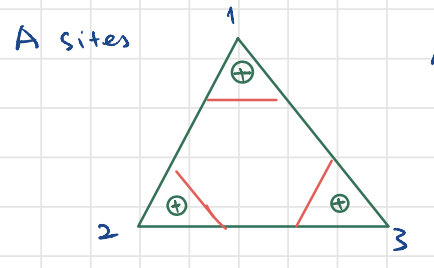
Likewise, for the triangle of B sites, the phase picked up has the same magnitude but opposite sign, so we have complex hopping for NNN
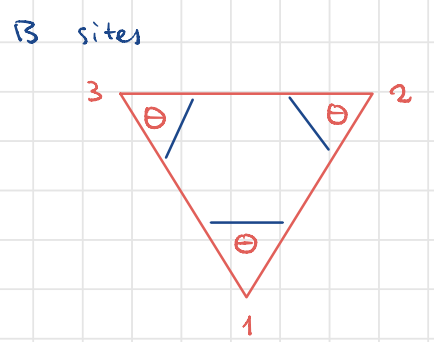
Note that the phase would be zero for the hexagon, enclosed by 6 NN hoppings. So the NN hopping remains unchanged.
Then we have
Denote
we have, for the NNN term on A-sublattice
Likewise, for B-sublattice
The consequence of the new Hamiltonian can be seen by lienearzing the Hamiltonian near
where
Non-zero, quantized Berry flux occurs when the two valleys have opposite masses.
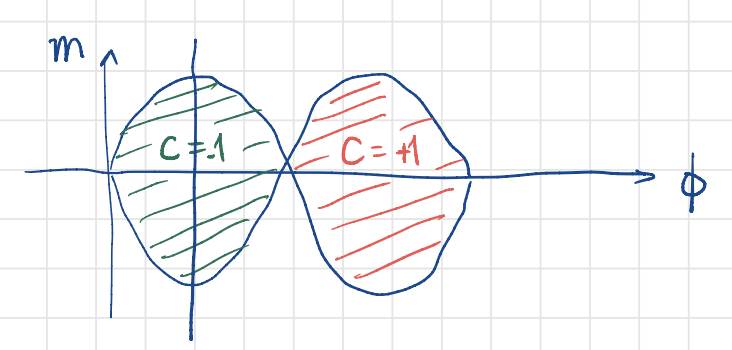
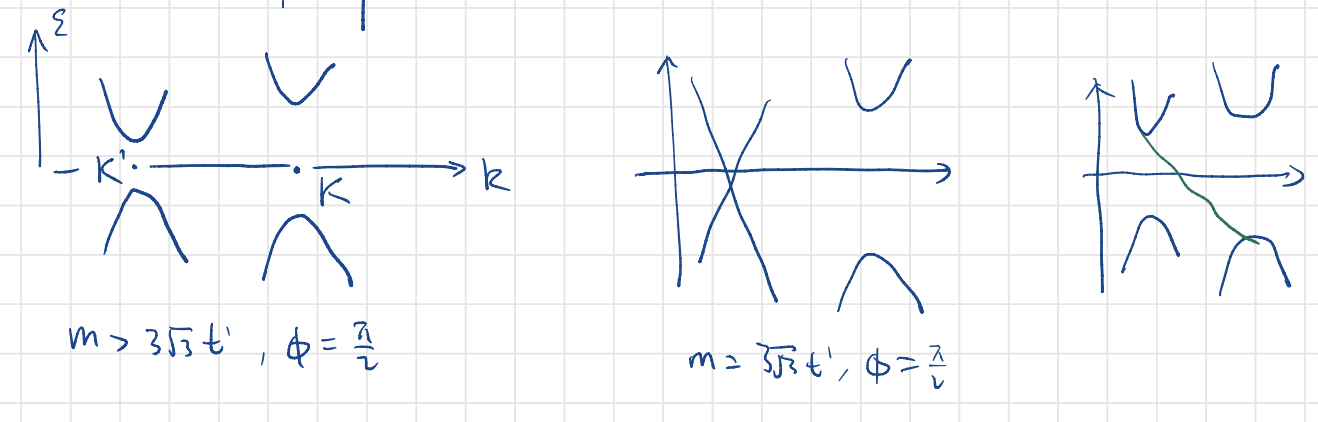
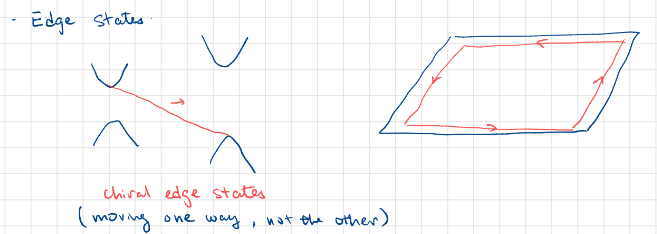
This leads to the quantum anomalous Hall effect (QAHE). There is an chiral edge state. Chiral here means the edge state moves one way, not the other. so there is not going to be backscattering. So the edge transport is insensitive to (elastic) scattering, as there can be no back scattering
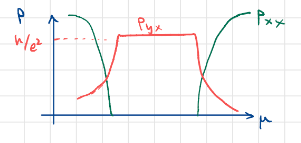
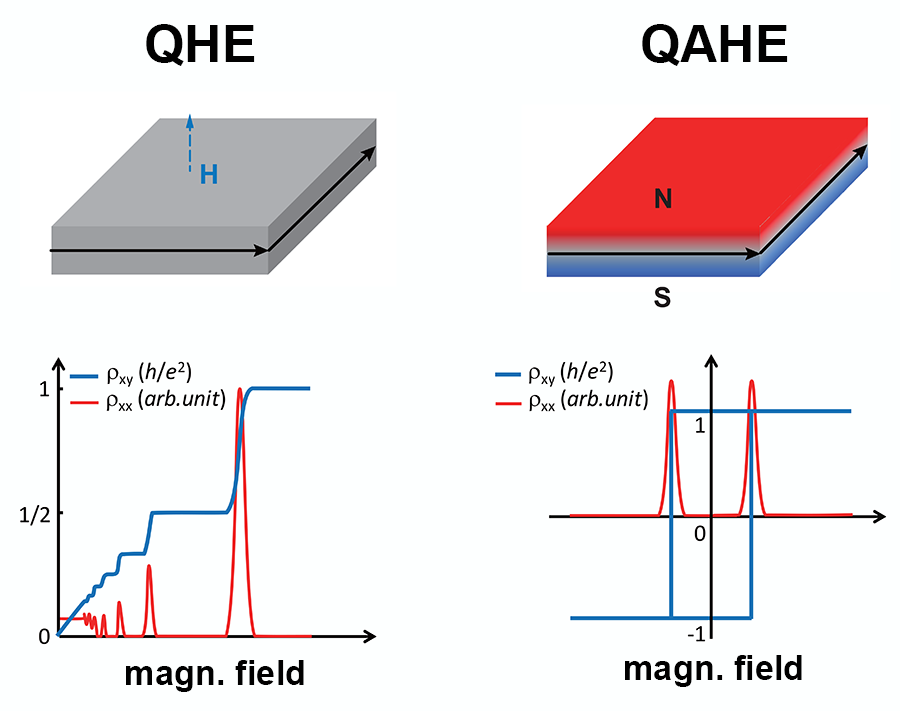
How to measure the QAHE?
where
Another way to understand the chirality. The grand potential is
So we have the Maxwell relation
or
We find that in the gap
So there must be a current circulation that produces the orbital magnetic momentum in the QAHE regime.
Final question, what is the geometric meaning of Chern number in this case?

It is easy to verify that
which is a map from the BZ (
which again forms a group by path composition (路径复合, jargon in algebraic topology), that is isomorphic to the integer group. Hence the Chern number.
Two 2D Hamiltonians can have vastly different appearance, but if they have the same Chern number, they are in the same equivalence class and have they same topology.