Lecture 19

04/27/23, Th.

Today

• Kane-Mele model of 2D TI

• Topological insulator and semimetals

• Integer quantum Hall effect

1. Kane-Mele model of 2D TI

Consider two copies the Haldane models, which are time-reversed images of each other. As the Berry curvature or flux changes sign under time reversal,

So the combined system has no berry flux through the Brillouin zone. But there will be a pair of degenerate edge states that are Kramer's pair of each other.

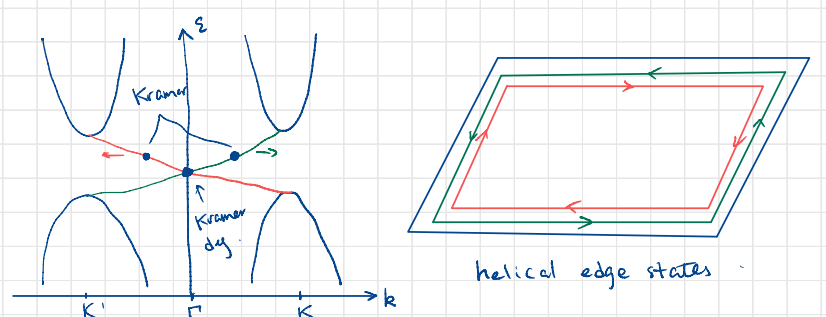
Kramers' degeneracy comes from time-reversal symmetry. For spin-1/2, the time-reversal operation is

where $K$$K$ takes the complex conjugate of what ever number follows it. So

which is a Bloch function transforms as the irreducible representation (不可约表示) of $-\mathit{k}$$-\boldsymbol k$, so that

If the Hamiltonian has time-reversal symmetry, this means

Therefore, ${\psi }_{\mathit{k}}$$\psi_\boldsymbol k$ and $\mathrm{\Theta }{\psi }_{\mathit{k}}$$\Theta \psi_\boldsymbol k$ are degenerate and called a Kramer's pair. This degeneracy is called the Kramer's degeneracy.

This is precisely what the Kane-Mele model does, except the staggered magnetic flux is replaced by spin-orbit coupling. To write down the Kane-Mele model, we need three sets of Pauli matrices

$\sigma$$\sigma$ : sublattice $A,B$$A, B$ $\tau$$\tau$ : valley $K,K$$K, K$ ' $s$$s$ : spin $\uparrow ,\downarrow$$\uparrow, \downarrow$

So the low-energy effective Hamiltonian is

So the bulk spectrum is two-fold degenerate within each valley $\tau$$\tau$

Initially, Kane and Mele thought there will be a quantized spin current, so they give the name quantum spin Hall effect, describable by a spin Chern number

But the problem is if spin is not good quantum number (with symmetry being broken ever so slightly), so it cannot be a conserved quantity and the quantization gets destroyed.

It turns out, what is important is the Kramer's degeneracy protected by TR symmetry. As edge states ${\psi }_{\mathit{k}}$$\psi_{\boldsymbol k}$ and $\mathrm{\Theta }{\psi }_{\mathit{k}}$$\Theta\psi_{\boldsymbol k}$ have exactly opposite spins, if the impurity has time reversal symmetry there will be no back scattering. This pair of counter-propagating edge states related by TR, and are called helical edge states.

It is argued that even with strong disorder, the reflected amplitude must be odd under time-reversal symmetry, so it should be zero. The consequence is that the helical edge states are immune to strong disorder and Anderson localization. From the Landauer formula, we have

The helical edge states protected by the time-reversal symmetry. But what is the bulk topological invariant? The exact formulation is algebraically involved. We will get a first idea with a pictorial argument.

Consider the edge states. We note that if $-\mathit{k}=\mathit{k}$$-\boldsymbol k = \boldsymbol k$, then obviously the bands at $\mathit{k}$$\boldsymbol k$ are two-fold degenerate. The quasimomenta that satisfy this relation

where $\mathit{g}$$\boldsymbol g$ is a reciprocal lattice vector, are called time-reversal invariant (quasi)momenta (well, apart from an $\hslash$$\hbar$). Then at these TRIM, the edge states are doubly degenerate due to the Kramer degeneracy. If there spin-orbit interaction, the degeneracy is generally lifted, and each band is spin polarized.

In the case of a 2D insulator, its edge Brillouin zone has two TRIMS: $\overline{k}=0,\pi$$\bar k=0,\pi$. The key is, how the doubly degenerate bands at $\overline{k}=0$$\bar k=0$ and $\overline{k}=\pi$$\bar k=\pi$ are connected by spin polarized bands. In fact there are only two scenarios, as depicted in the cartoon below.

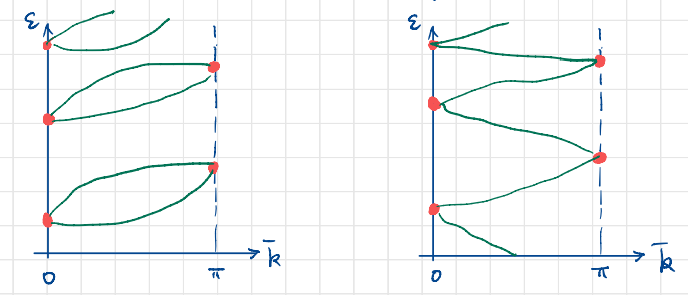
The case on the left is considered trivial, because it can be continuously deformed into an insulator, by changing the chemical potential for example. The case on the right is the topological. So from the edge state point of view, the topology protected by time reversal symmetry has two distinct classes, entailing a ${\mathbb{Z}}_2$$\mathbb Z_2$ classification.

In bulk ${\mathbb{Z}}_2$$\mathbb Z_2$ invariant can be defined with the knowledge of occupied wavefunctions for systems with time-reversal symmetry. It can be simplified for systems with inversion symmetry, for which

where ${\mathit{k}}_0$$\boldsymbol k_0$ are TRIM of the bulk Brillouin zone, and $\delta ({\mathit{k}}_0)$$\delta (\boldsymbol k_0)$ is the parity of occupied states at ${\mathit{k}}_0$$\boldsymbol k_0$

If $\nu =1$$\nu=1$, the system is then a topological insulator, with topologically protected edge/surface states. If $\nu =0$$\nu=0$, the system is then called a trivial (平庸) insulator.

2. Weyl semimetal

A minimal model for a Weyl semimetal can be written again in a two-band Hamiltonian.

where

Here $\chi =\pm 1$$\chi=\pm 1$ corresponding to the chirality of a Weyl node. For example with ${\mathit{k}}_0=(0,0,k_0)$$\boldsymbol k_0=(0,0,k_0)$,

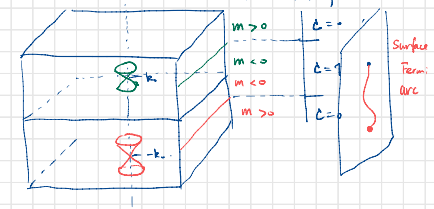
The 2D Brillouin zone with $k_z\in [-k_0,k_0]$$k_z\in [-k_0,k_0]$ gives a Chern insulator (quantum anomalous hall insulator), with a chiral edge mode on the surface. Out side this interval, the 2D Brillouin zone for each $k_z$$k_z$ is trivial. So the surface Fermi line terminate at ${\overline{k}}_z=\pm k_0$$\bar k_z=\pm k_0$, forming a finite surface Fermi arc.

I will stop here our discussion on these topics in view of time, and switch gear to the more traditional topic of another topological system.

3. Integer quantum Hall effect

3.1 Phenomenology

The quantum Hall effect is typically induced in a 2-dimensional electron gas (2DEG) by a perpendicular magnetic field.

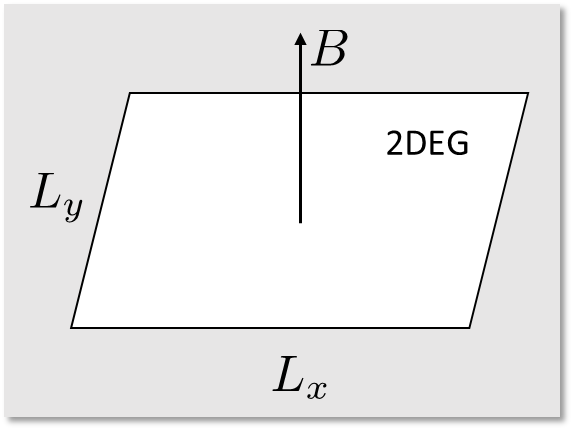
It is called quantum Hall effect because the Hall conductivity is quantized

where the filling factor $\nu$$\nu$ is an integer.

In a typical Hall measurement, we have current flowing in the longitudinal direction, with the transverse current to be zero (open circuit).

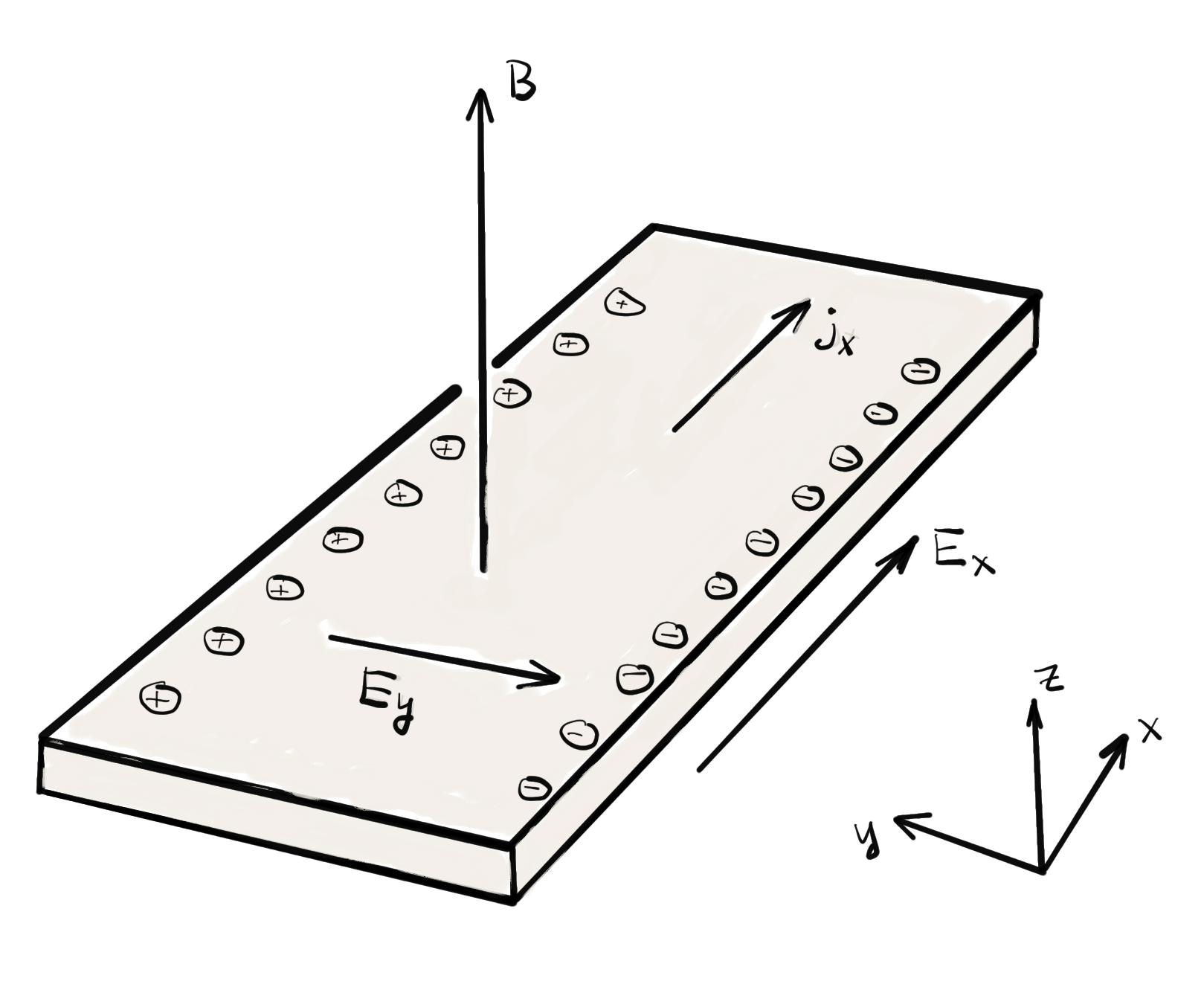
In Drude theory

In steady state $\dot{\mathit{p}}=0$$\dot{\boldsymbol p}=0$ so,

where the cyclotron frequency is

Setting $p_y=0$$p_y=0$, we have

That is

Note the Hall resistivity is independent of scattering time.

In the quantum Hall measurement, the Hall resistance $R_H$$R_H$ is quantized

so the filling factor $\nu$$\nu$ is

the number of electrons per flux quantum threading the system.

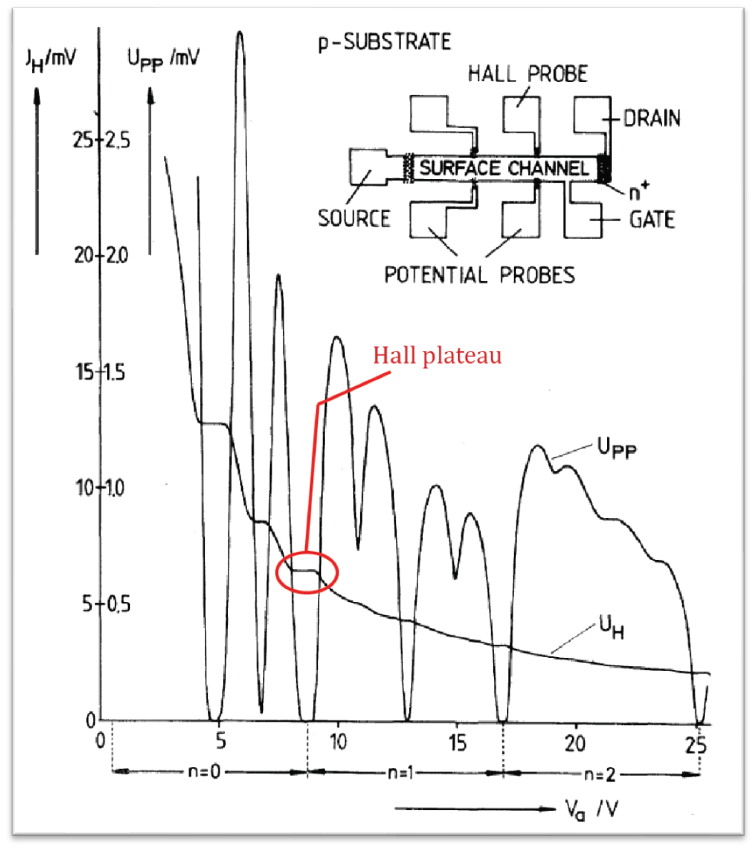
At the Hall plateau

• there is precice quantizatoin of $U_H$$U_H$ or $R_H$$R_H$

• ${\sigma }_{xx}=0$$\sigma_{xx}=0$ indicating a insulating phase.

The question is: why the precise quantization? By now, you probably have guessed it is the same thing as the quantum anomalous Hall effect. And you are right. But let's see how this can be understood.

3.2 Disorder is necessary

A curious thing about the integer quantum Hall effect is that disorder is important! Let's consider a perfect 2DEG that is translationally and rotationally invariant. In the lab frame

There is no current.

Now in a moving frame with a constant velocity $-\mathit{v}$$-\boldsymbol v$, there appears to be current

and the electric and magnetic fields of the Lorentz boost is

such that

There can be no quantization! As the argument only involves density, it applies whether the theory is quantum or classical.

To have quantization, we must break the Lorentz covariance. We need inhomogeneity (disorder) to break the translational or rotational invariance.

3.3 Landau levels

Choosing the Landau gauge for $\mathit{B}=-B\hat{z}$$\boldsymbol B= -B\hat z$

the single-electron Hamiltonian reads

which is translationally invariant in $y$$y$-direction. So the wavefunction can be written as

where

So $H_k$$H_k$ looks exactly like a Hamiltonian of a 1DHO centered at $x_k$$x_k$ with a characteristic frequency ${\omega }_c$$\omega_c$. So the energies of these discrete Landau levels are

which is highly degenerate as it is $k$$k$ independent.

We use $n$$n$ as the quantum number for the energy levels of the 1DHO, and the wavefunction is

where $H_n(z)$$H_n(z)$ is the Hermite polynomial.

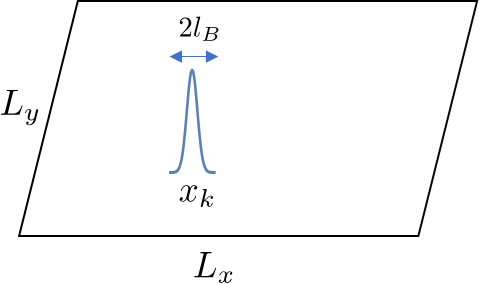
What exactly is the degeneracy of a Landau level? We need $x_k\in [0,L]$$x_k\in[0,L]$,

States on the left and right edges can have vastly different k values. Noting $k$$k$ is $k_y$$k_y$, the number of states in a LL is

Thus, there there is one state per flux quantum in an LL. So when $\nu$$\nu$ takes integer values, the Landau levels are either fully filled or empty in the ground state. Thus, the quantum Hall states are insulating, incompressible, like a band insulator.

Consider a wavepacket and its time evolution is clearly

Now consider

so the motion is clearly periodic, like the classical cyclotron orbit motion.

3.4 Current response

Now we want to calculate the current response of a quantum Hall system. We will restrict ourselves to the lowest Landan level (LLL)

The current density for a given $k$$k$ is

So the current in y-direction is

Here, the canonical momentum in y-direction $\hslash k$$\hbar k$ is exactly cancelled by the vector potential, so the mechanical momentum vanishes.

There is no current in the ground state, for sure. This is expected since ${\epsilon }_{nk}$$\varepsilon_{nk}$ is independent of $k$$k$, so the electron group velocity is zero, in any LL.

But, this independence of energy on $k$$k$ comes from the fact that energy is independent of $x_k$$x_k$. This can be immediately changed if an electric field is applied

which also preserves translation invariance in $y$$y$-direction.

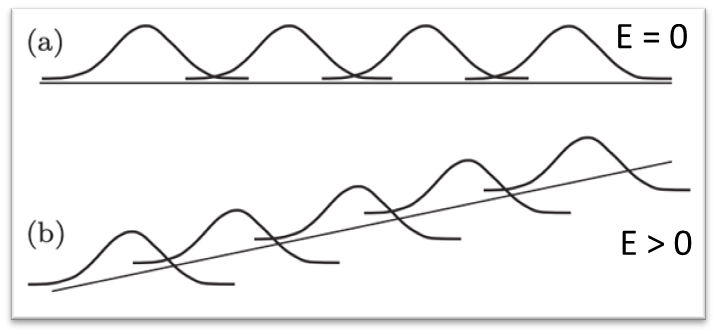
The Hamiltonian can be re-written

where we have new guiding center

and introduced a drift velocity

So the LL energies become

So the current becomes

So the current density in y direction is

So

So the filled LLL has a quantized Hall conductivity.

We will then try and understand the topological nature of the quantized Hall effect, by figuring out the bulk topological invariant and the corresponding edge states.