Electrons are right at the heart of current research efforts aiming to understand condensed matter materials, including insulator, metals, topological materials, superconductors, and many more. State-of-the-art first-principles methods provide us with an accurate description of the basic electronic structure of a broad range of materials. And yet, to understand the physical properties of real materials, it is necessary to take one step above the basic, and to take into account a little extra physics. Our research is thus geared toward bridging the gap between basics electronic structure and physical properties of real materials. A few examples of such problems and on-going projects are described below.
Physical effects of Berry phase
Berry phase arises when quantum mechanical system evolves in a cyclic fashion in a parameter space. The Brillouin zone is a natural parameter space for an electron in a crystal. It is known the Berry phase leads to many an exotic behavior to electrons, such anomalous Hall effect, and various topological transport phenomena. We develop computational tools to compute in order to assay materials for these fascinating properties related to Berry phase, and to help experimentalists understand related measurements.
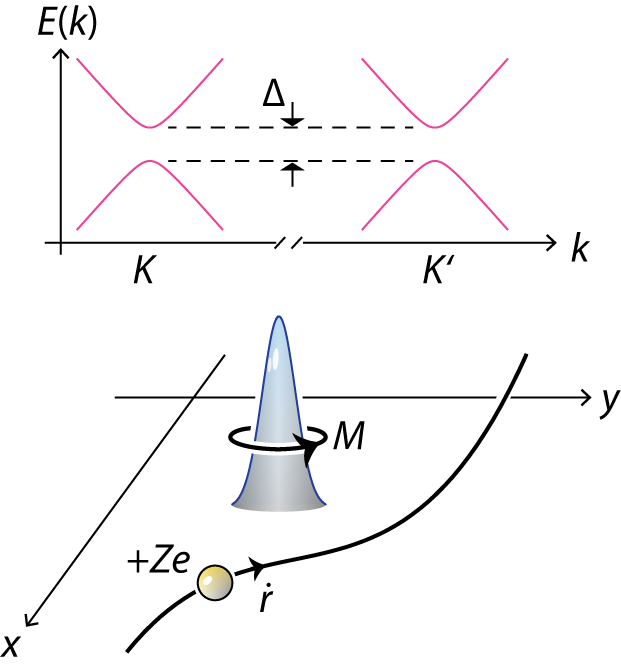
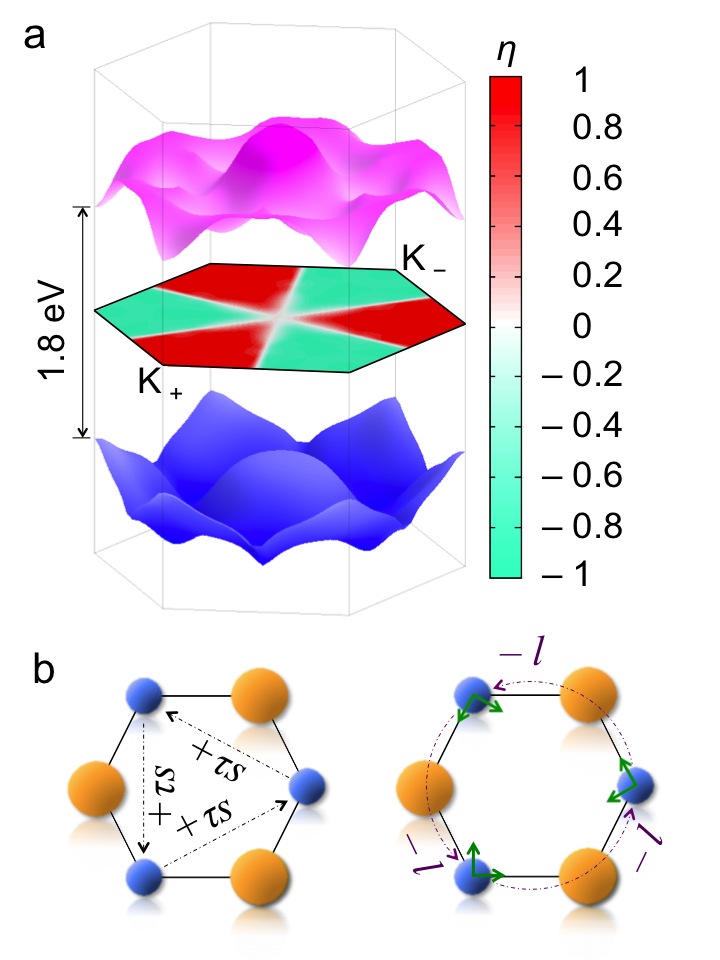
In earlier work we have discovered the first valleytronic material, MoS2, which shows perfect valley-selective circular dichroism and optically induced Hall effect. We have derived rigorously from the quantum mechanical framework how Berry phase figures in the 2nd-order effective mass theory when a Bloch electron is subject to an external potential (e.g., an impurity potential). Currently, we are working on a few closely related problems, such orbital magnetization (with potential complication from interaction).
Electronic transport
Electrons move in a material and lead to an electric current, which is about the most elementary and fundamental property of materials. Electric conduction is the most frequently used probe to examine material physics. It is, however, very challenging to compute the conductivity of a material — embarrassingly so, providing our access to high-quality electronic structure of many materials. The cause for such difficulty is multifactorial. For example, it is known that resistance can arise from scattering with impurities in a material. It is highly nontrivial to compute the correction to conductivity for real materials beyond the the Boltzamann formalism, i.e., quantum interference. In the setting of optical current generation, it is sometimes necessary to go beyond the linear response when nonlinear current becomes the leading order effect.

We have developed the codes to compute the anomalous Hall current, based on electronic structure of real materials. In a recent work, we have developed a code to compute the nonlinear photocurrent, which allowed us to analyze the optical response of a Weyl semimetal TaIrTe4, along with our experimental collaborators. Presently, we are working toward packages for computing nonlinear current and for general band structures, and efficient algorithms for computing quantum correction to the Boltzmann conductivity.